| № п\п | Внесено удобрений, ц на 1 га, 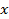 | Урожайность, ц с1 га, 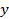 | 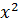 | 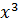 | 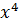 | 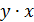 | 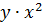 | 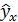 |
| 6,2 8,5 10,4 11,9 13,0 | ||||||||
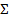 | 50,0 |
Поданным табл. 4.3 система нормальных уравнений составит:
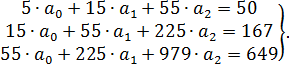
Решая ее методом определителей, получим: 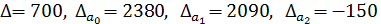 . Откуда параметры искомого уравнения составят:
. Откуда параметры искомого уравнения составят: 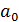 == 3,4;
== 3,4; 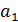 =2,986;
=2,986; 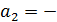 0,214, а уравнение параболы второй степени примет вид
0,214, а уравнение параболы второй степени примет вид
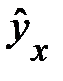
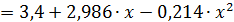 .
.
Подставляя в это уравнение последовательно значения х, найдем теоретические значения 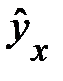 (см. табл. 4.3, гр. 9).
(см. табл. 4.3, гр. 9).
Каквидно из табл. 2.3, уравнение параболы второго порядка хорошо описывает рассматриваемую зависимость. Сумма квадратов отклонений остаточных величин 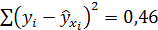 . Ввиду того, что данные табл. 4.3 демонстрируют лишь сегмент параболы второго порядка, то рассматриваемая зависимость может быть охарактеризована и другой функцией. Используя, в частности, степенную функцию
. Ввиду того, что данные табл. 4.3 демонстрируют лишь сегмент параболы второго порядка, то рассматриваемая зависимость может быть охарактеризована и другой функцией. Используя, в частности, степенную функцию 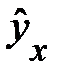
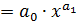 ,было получено уравнение регрессии
,было получено уравнение регрессии 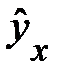
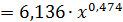 . Для него
. Для него 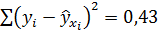 , что означает еще лучшую сходимость фактических и расчетных значений y.
, что означает еще лучшую сходимость фактических и расчетных значений y.
Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу: 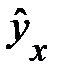
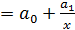 .
.
Она может быть использована не только, как уже указывалось в параграфе (2.2), для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микроуровне, но и на макроуровне. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы у:
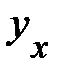
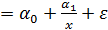 .
.
Английский экономист А. В. Филлипс, анализируя данные
более чем за 100-летний период, в конце 50-х гг. XX в. установил
обратную зависимость процента прироста заработной платы от
уровня безработицы.
Для равносторонней гиперболы вида №№, заменив 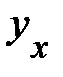
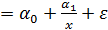 , заменив
, заменив  на z, получим линейное уравнение регрессии
на z, получим линейное уравнение регрессии 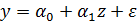 оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
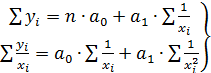 .
.
При 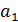 > 0 имеем обратную зависимость, которая при
> 0 имеем обратную зависимость, которая при 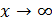 характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр a. Так, для кривой Филипса
характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр a. Так, для кривой Филипса
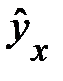
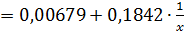 величина параметра a, равная 0,00679, означает, что с ростом уровня безработицы темп прироста заработной платы в пределе стремится к нулю. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.
величина параметра a, равная 0,00679, означает, что с ростом уровня безработицы темп прироста заработной платы в пределе стремится к нулю. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.
При 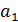 < 0 имеем медленно повышающуюся функцию с верхней асимптотой при
< 0 имеем медленно повышающуюся функцию с верхней асимптотой при 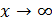 , т. е. с максимальным предельным
, т. е. с максимальным предельным
уровнем у, оценку которого в уравнении 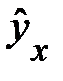
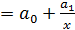 дает пара метр
дает пара метр 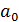 .
.
Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание подобного рода взаимосвязей получило название кривых Энгеля. В1857 г. немецкий статистик Э. Энгель на основе исследования семейных расходов сформулировал закономерность — с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается. Соответственно с увеличением дохода доля доходов, расходуемых на непродовольственные товары, будет возрастать. Однако это увеличение не беспредельно, ибо на все товары сумма долей не может быть больше единицы, или 100%, а на отдельные непродовольственные товары этот предел может характеризоваться величиной параметра а для уравнения вида
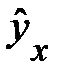
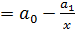 ,
,
где у — доля расходов на непродовольственные товары;
х — доходы (или общая сумма расходов как индикатор дохода).
Правомерность использования равномерной гиперболы 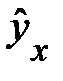
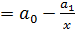 для кривой Энгеля довольно легко доказывается.
для кривой Энгеля довольно легко доказывается.
Соответственно можно определить границу величины дохода, дальнейшее увеличение которого не приводит с росту доли расходов на отдельные непродовольственные товары.
Вместе с тем равносторонняя гипербола 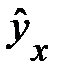
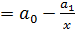 не является единственно возможной функцией для описания кривой Энгеля. В 1943 г. Уоркинг и в 1964 г. Лизер для этих целей использовали полулогарифмическую кривую
не является единственно возможной функцией для описания кривой Энгеля. В 1943 г. Уоркинг и в 1964 г. Лизер для этих целей использовали полулогарифмическую кривую 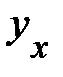
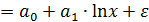 .
.
Заменив 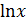 на z,опять получим линейное уравнение:
на z,опять получим линейное уравнение: 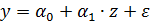 . Данная функция, как и предыдущая, линейна по параметрам и нелинейна по объясняющей переменной х. Оценка параметров
. Данная функция, как и предыдущая, линейна по параметрам и нелинейна по объясняющей переменной х. Оценка параметров 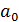 и
и 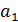 может быть найдена МНК. Система нормальных уравнений при этом окажется следующей:
может быть найдена МНК. Система нормальных уравнений при этом окажется следующей:
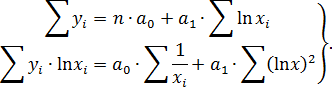
Применим полулогарифмическую функцию зависимости доли расходов на товары длительного пользование в общих расходах семьи от дохода семьи (табл. 4.4).
Таблица 4.4
Доля расходов на товары длительного пол в зависимости от дохода семьи
| Среднемесячный доход семьи, тыс. долл. США, x | ||||||
| Процент расходов на товары длительного пользования, y | 13,4 | 15,4 | 16,5 | 18,6 | 19,1 |
Суммы, необходимые для расчета, составили:
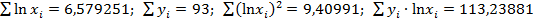 .
.
Решая систему нормальных уравнений
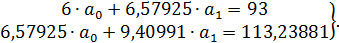
мы получили уравнение регрессии 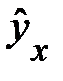
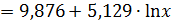 , которое достаточно хорошо описывает исходные соотношения дохода семьи и доли расходов на товары длительного пользования, что видно из сравнения фактических и теоретических значений у:
, которое достаточно хорошо описывает исходные соотношения дохода семьи и доли расходов на товары длительного пользования, что видно из сравнения фактических и теоретических значений у:
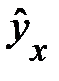 | 9,9 | 13,4 | 15,5 | 17,0 | 18,1 | 19,1 | Сумма |
y 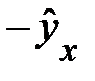 | 0,1 | 0,0 | -0,1 | -0,5 | 0,5 | 0,0 | 0,0 |
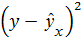 | 0,01 | 0,0 | 0,01 | 0,25 | 0,25 | 0,0 | 0,52* |
*При более точном подсчете 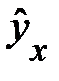 эта величина составит 0,4864. эта величина составит 0,4864. |
Возможны и иные модели, нелинейные по объясняющим переменным. Например, 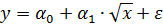 . Соответственно система нормальных уравнений для оценки параметров составит:
. Соответственно система нормальных уравнений для оценки параметров составит:
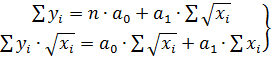 .
.
Уравнения с квадратными корнями использовались в исследованиях урожайности, трудоемкости сельскохозяйственного производства. В работе Н. Дрейпера и Г. Смита справедливо отмечено, что если нет каких-либо теоретических обоснований в использовании данного вида кривых, то основная цель подобных преобразований состоит в том, чтобы для преобразованных переменных получить более простую модель регрессии, чем для исходных данных.
Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и
нелинейные модели внутренне нелинейные. Если нел инейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция:
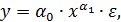
где 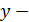 спрашиваемое количество;
спрашиваемое количество;
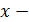 цена;
цена;
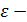 случайная ошибка.
случайная ошибка.
Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры а и b не аддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к л шейному виду:
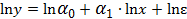 .
.
Соответственно оценки параметров a и b пут быть найдены МНК. В рассматриваемой степенной функции предполагается, что случайная ошибка е мультипликативно связана с объясняющей переменной х. Если же модель представить в виде 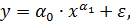 то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид.
то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид.
Внутренне нелинейной будет и модель вила
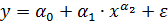
или модель
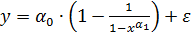 ,
,
ибо эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам.
В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейные, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель 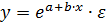 ,ибо логарифмируя ее по натуральному основанию, получим линейную форму модели
,ибо логарифмируя ее по натуральному основанию, получим линейную форму модели
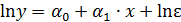 .
.
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях. Однако гораздо большее распространение получили модели, приводимые к линейному виду. Решение такого типа моделей реализовано в стандартных пакетах прикладных программ. Среди них, в частности, можно назвать и обратную модель вида
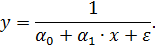
Обращая обе части равенства, получим линейную форму модели для переменной  :
:
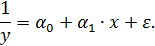
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция 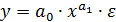 .Связано это с тем, что параметр
.Связано это с тем, что параметр 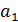 в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента
в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента 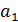 показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %. Так, если зависимость спроса от цен характеризуется уравнением вида
показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %. Так, если зависимость спроса от цен характеризуется уравнением вида 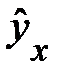
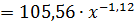 , то, следовательно, с увеличением цен на 1 % спрос снижается в среднем на 1,12 %. О правомерности подобного истолкования параметра
, то, следовательно, с увеличением цен на 1 % спрос снижается в среднем на 1,12 %. О правомерности подобного истолкования параметра 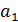 для степенной функции
для степенной функции 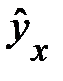
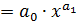 можно судить, если рассмотреть форм
можно судить, если рассмотреть формулу расчета коэффициента эластичности
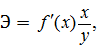
где 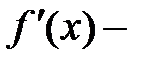 первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Для степенной функции она составит: 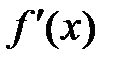
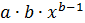 . Соответственно коэффициент эластичности окажется равным:
. Соответственно коэффициент эластичности окажется равным:
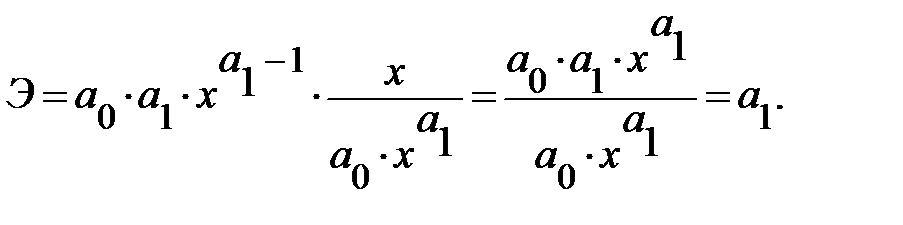
Коэффициент эластичности, естественно, можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру 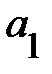 . В других функциях коэффициент эластичности зависит от значений фактора х. Так, для линейной регрессии
. В других функциях коэффициент эластичности зависит от значений фактора х. Так, для линейной регрессии 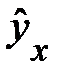
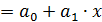 функция и эластичность следующие:
функция и эластичность следующие:
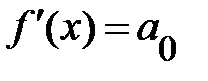 и
и 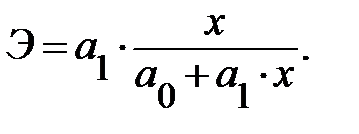
В силу того что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле
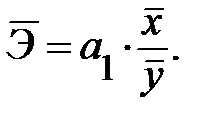
Для оценки параметров степенной функции 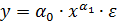 применяется метод наименьших квадратов к линеаризованному уравнению
применяется метод наименьших квадратов к линеаризованному уравнению 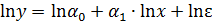 , т.е. решается система нормальных уравнений:
, т.е. решается система нормальных уравнений:
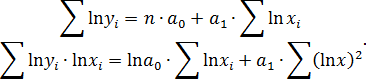
Параметр 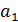 определяется непосредственно из системы, а параметр
определяется непосредственно из системы, а параметр 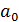 — косвенным путем после потенцирования величины
— косвенным путем после потенцирования величины 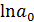 . Так, решая систему нормальных уравнений зависимости спроса от цен, было получено уравнение
. Так, решая систему нормальных уравнений зависимости спроса от цен, было получено уравнение 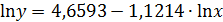 Если потенцировать его, получим:
Если потенцировать его, получим:
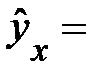
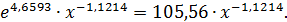
Поскольку параметр 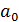 экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически линейной. В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром
экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически линейной. В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром 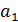 < 0, а эластичность предложения:
< 0, а эластичность предложения: 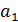 > 0.
> 0.
Поскольку коэффициенты эластичности представляют экономический интерес, а виды моделей не ограничиваются только степенной функцией, приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии (табл. 4.5).
Таблица 4.5
Коэффициенты эластичности для ряда математических функций
Вид функции, 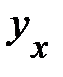 | Первая производная, 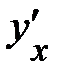 | Коэффициенты эластичности, 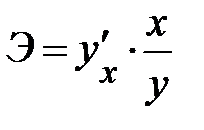 |
Линейная 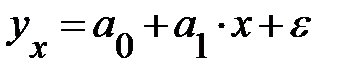 | 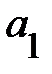 | 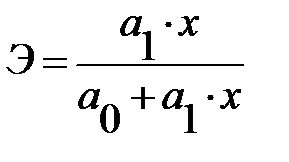 |
Парабола второго порядка 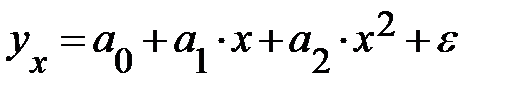 | 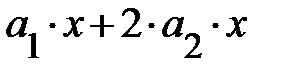 | 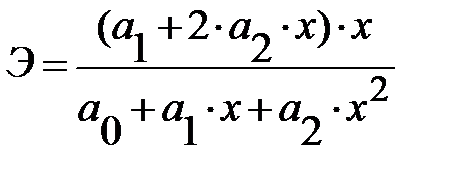 |
Гипербола 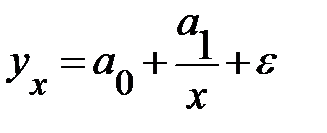 | 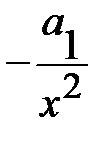 | 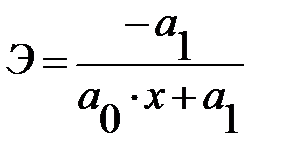 |
Показательная 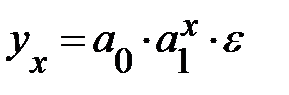 | 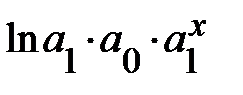 | 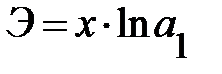 |
Степенная 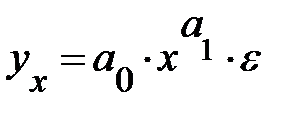 | 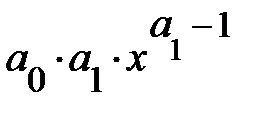 | 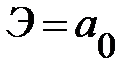 |
Полулогарифмическая 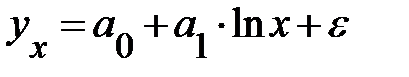 | 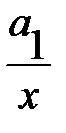 | 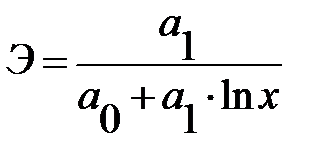 |
Логарифмическая 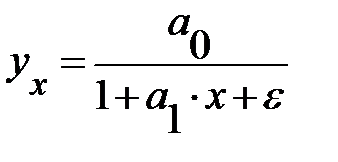 | 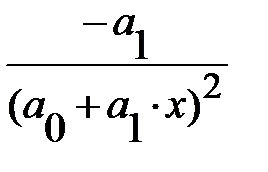 | 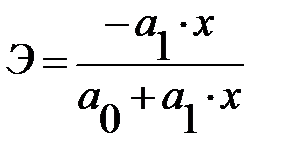 |
Обратная 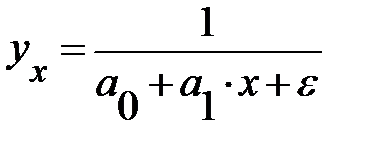 | 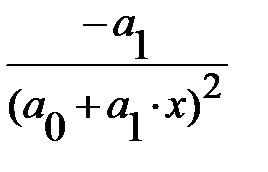 | 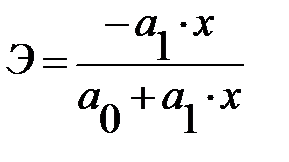 |
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли кто будет определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %. Или, например, на сколько процентов изменится урожайность пшеницы, если качество почвы, измеряемое в баллах, изменится на 1 %. В такой ситуации степенная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наименьшего значения остаточной вариации), не может быть экономически интерпретирована. Например, изучая соотношение ставок межбанковского кредита у (в процентах годовых) и срока его предоставления х (в днях), было получено уравнение регрессии 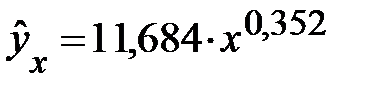 с очень высоким показателем корреляции (0,9895). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция
с очень высоким показателем корреляции (0,9895). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция 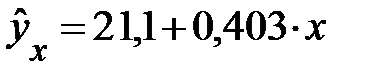 , имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает в процентных пунктах изменение ставок кредита с увеличением срока их предоставления на один день.
, имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает в процентных пунктах изменение ставок кредита с увеличением срока их предоставления на один день.
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия 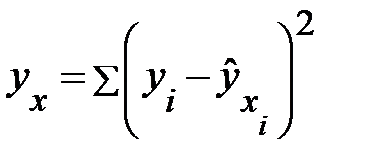 , то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е.
, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. 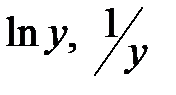 . Так, в степенной функции
. Так, в степенной функции 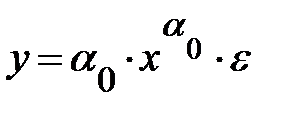 МНК применяется к преобразованному уравнению
МНК применяется к преобразованному уравнению 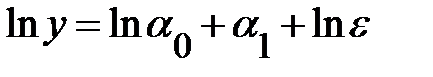 .
.
Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах.
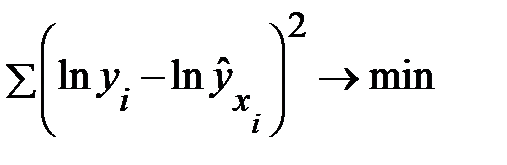 .
.
Соответственно если в линейных моделях (включая нелинейные по переменным) 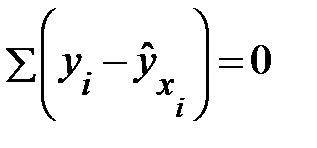 , то в моделях, нелинейных по оцениваемым параметрам,
, то в моделях, нелинейных по оцениваемым параметрам,
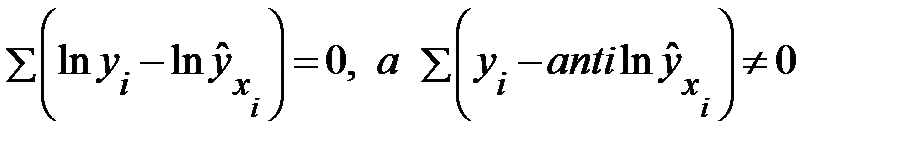 .
.
Вследствие этого оценка параметров для линеаризуемых функций МНК оказываются несколько смещенной.
Возьмем, например, показательную кривую: 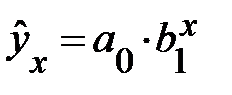 или равносильную ей экспоненту
или равносильную ей экспоненту 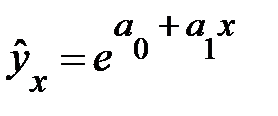 . Прологарифмировав, имеем:
. Прологарифмировав, имеем:
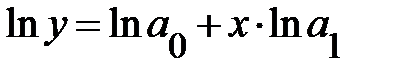 .
.
Применяя МНК, минимизируем 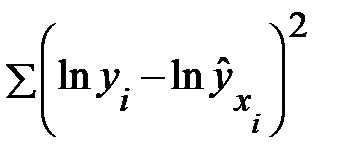 . Система нормальных уравнений составит:
. Система нормальных уравнений составит:
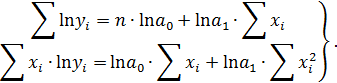
Из первого уравнения видно, что
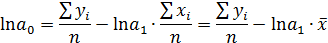
Предположим, что фактические данные сложились так, что 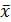 . Тогда
. Тогда 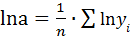 или
или 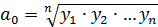 , т. е. параметр
, т. е. параметр 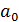 представляет собой среднюю геометрическую из значений переменной у. Между тем в линейной зависимости
представляет собой среднюю геометрическую из значений переменной у. Между тем в линейной зависимости 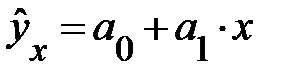 при
при 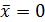 параметр
параметр
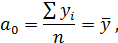
т. е. средней арифметической. Поскольку средняя геометрическая всегда меньше средней арифметической, то и оценки параметров, полученные из минимизации 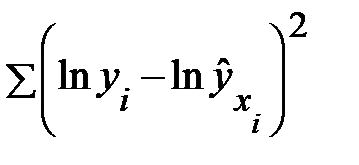 , будут несколько смещены (занижены).
, будут несколько смещены (занижены).
Практическое применение экспоненты возможно, если результативный признак не имеет отрицательных значений. Поэтому если исследуется, например, финансовый результат деятельности предприятий, среди которых наряду с прибыльными есть и убыточные, то данная функция не может быть использована. Если экспонента строится как функция выравнивания по динамическому ряду для характеристики тенденции с постоянным темпом, то 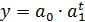 , где у — уровни динамического ряда; t - хронологические даты, параметр b означает средний за период коэффициент роста. В уравнении
, где у — уровни динамического ряда; t - хронологические даты, параметр b означает средний за период коэффициент роста. В уравнении 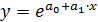 этот смысл приобретает величина антилогарифма параметра
этот смысл приобретает величина антилогарифма параметра 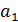 .
.
При исследовании взаимосвязей среди функций, использующих 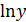 , в эконометрике преобладают степенные зависимости — это и кривые спроса и предложения, и кривые Энгеля, и производственные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, и зависимость валового национального дохода от уровня занятости.
, в эконометрике преобладают степенные зависимости — это и кривые спроса и предложения, и кривые Энгеля, и производственные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, и зависимость валового национального дохода от уровня занятости.
В отдельных случаях может использоваться и нелинейная модель вида
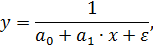
так называемая обратная модель, являющаяся разновидностью гиперболы. Но если в равносторонней гиперболе 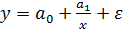 преобразованию подвергается объясняющая переменная
преобразованию подвергается объясняющая переменная 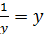 и
и 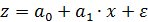 .то для по. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных величин
.то для по. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных величин  , а именно:
, а именно: 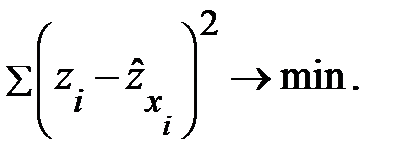
Соответственно
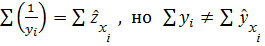 .
.
Проанализируем зависимость рентабельности продукции от ее трудоемкости по данным семи предприятий (табл. 4.6).
Таблица 4.6
Зависимость рентабельности продукции y (%) от ее
трудоемкости x (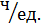 )
)
| x | y | 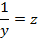 |  | 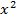 | 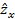 | 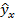 | 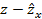 | 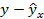 |
| 1,0 | 0,0312 | 0,0312 | 1,00 | 0,0285 | 35,1 | 0,0027 | -3,1 | |
| 1,2 | 0,0357 | 0,0428 | 1,44 | 0,0341 | 29,3 | 0,0016 | -1,3 | |
| 1,5 | 0,0455 | 0,0682 | 2,25 | 0,0424 | 23,6 | 0,0031 | -1,6 | |
| 2,0 | 0,0500 | 0,1000 | 4,00 | 0,0563 | 17,7 | -0,0063 | 2,3 | |
| 2,5 | 0,0625 | 0,1563 | 6,25 | 0,0703 | 14,2 | -0,0078 | 1,8 | |
| 2,7 | 0,0667 | 0,1800 | 7,29 | 0,0758 | 13,2 | -0,0091 | 1,8 | |
| 3,0 | 0,1000 | 0,3000 | 9,00 | 0,0842 | 11,9 | 0,0158 | -1,9 | |
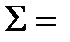 13,9 13,9 | 0,3916 | 0,8785 | 31,23 | 0,3936 | 145,0 | 0,0000 | -2,0 |
Для оценки параметров исследуемой функции 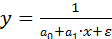 по МНК система нормальных уравнений примет вид:
по МНК система нормальных уравнений примет вид:
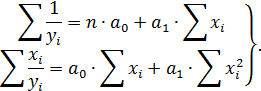
Исходя из данных табл. 2.6, имеем:
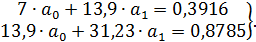
Решая эту систему уравнений, получим оценки параметров искомой функции: 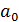 = 0,0007;
= 0,0007; 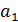 = 0,0278. Соответственно уравнение регрессии составит:
= 0,0278. Соответственно уравнение регрессии составит:
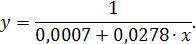
Сравним последние две графы табл. 2.6. Получим 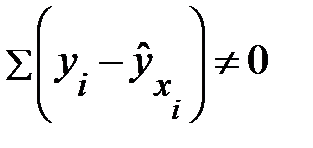 , тогда как для обратных значений эта величина равна нулю. Кроме того, заметим, что положительные отклонения фактических и теоретических обратных значений сменяются на отрицательные значения для аналогичных показателей по исходным данным. Уравнение отражает обратную связь рассматриваемых признаков: чем выше трудоемкость, тем ниже рентабельность. Поскольку данное уравнение линейно относительно величин
, тогда как для обратных значений эта величина равна нулю. Кроме того, заметим, что положительные отклонения фактических и теоретических обратных значений сменяются на отрицательные значения для аналогичных показателей по исходным данным. Уравнение отражает обратную связь рассматриваемых признаков: чем выше трудоемкость, тем ниже рентабельность. Поскольку данное уравнение линейно относительно величин  , то если обратные значения
, то если обратные значения  имеют экономический смысл, коэффициент регрессии
имеют экономический смысл, коэффициент регрессии 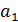 интерпретируется, так же как в линейном уравнении регрессии. Если, например, под y подразумеваются затраты на 1 руб. продукции, а под х — производительность труда (выработка продукции на одного работника), то обратная величина характеризует затратоотдачу и параметр
интерпретируется, так же как в линейном уравнении регрессии. Если, например, под y подразумеваются затраты на 1 руб. продукции, а под х — производительность труда (выработка продукции на одного работника), то обратная величина характеризует затратоотдачу и параметр 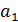 имеет экономическое содержание — средний прирост продукции в стоимостном измерении на 1 руб. затрат с ростом производительности труда на единицу своего измерения.
имеет экономическое содержание — средний прирост продукции в стоимостном измерении на 1 руб. затрат с ростом производительности труда на единицу своего измерения.
Уравнение вида 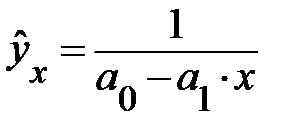 характеризует прямую зависимость результативного признака от фактора. Оно целесообразно при очень медленном повышении уровней результативного признака с ростом значений фактора.
характеризует прямую зависимость результативного признака от фактора. Оно целесообразно при очень медленном повышении уровней результативного признака с ростом значений фактора.
Возможно и одновременное использование логарифмирования, и преобразование в обратные величины: 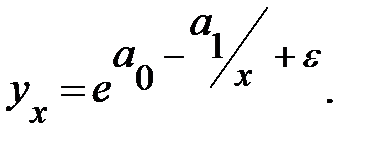 Прологарифмировав, получим:
Прологарифмировав, получим: 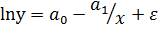 . Далее заменим
. Далее заменим  на z, и тогда для оценки параметров к линейному уравнению
на z, и тогда для оценки параметров к линейному уравнению 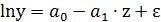 может быть применен МНК.
может быть применен МНК.
При всех положительных значениях х функция возрастает; при 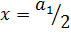 кривая имеет точку перегиба — ускоренный рост при
кривая имеет точку перегиба — ускоренный рост при 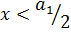 сменяется на замедленный рост при
сменяется на замедленный рост при 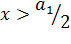 . Подобного типа функции используются при анализе статистических данных о бюджетах потребителей, где выдвигается гипотеза о существовании асимптотического уровня расходов, об изменении предельной склонности к потреблению товара, о существовании «порогового уровня дохода». В этом случае при
. Подобного типа функции используются при анализе статистических данных о бюджетах потребителей, где выдвигается гипотеза о существовании асимптотического уровня расходов, об изменении предельной склонности к потреблению товара, о существовании «порогового уровня дохода». В этом случае при 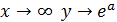 .
.
При использовании линеаризуемых функций, затрагивающих преобразования зависимой переменной у, следует особенно проверять наличие предпосылок
МНК (они будут рассмотрены в п. 3, 10), чтобы они не нарушались при преобразовании. При не линейных соотношениях рассматриваемых признаков, приводимых к линейному виду, возможно интервальное оценивание параметров нелинейной функции. Так, для показательной кривой 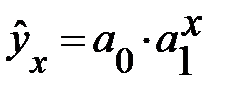 сначала строятся доверительные интервалы для параметров нового преобразованного уравнения
сначала строятся доверительные интервалы для параметров нового преобразованного уравнения 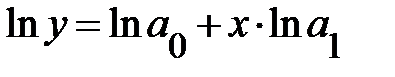 , т. е. для
, т. е. для 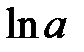 и
и 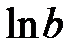 . Далее с помощью обратного преобразования определяются доверительные интервалы для параметров в исходном соотношении. В степенной функции
. Далее с помощью обратного преобразования определяются доверительные интервалы для параметров в исходном соотношении. В степенной функции 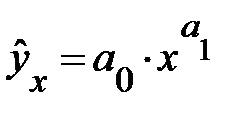 доверительный интервал для параметра b строится так же. как в линейной функции, т. е.
доверительный интервал для параметра b строится так же. как в линейной функции, т. е. 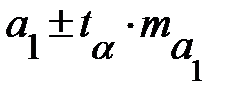 . Отличие состоит лишь в том. что при определении стандартной ошибки параметра b,
. Отличие состоит лишь в том. что при определении стандартной ошибки параметра b, 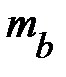 используются не исходные данные, а их логарифмы:
используются не исходные данные, а их логарифмы:
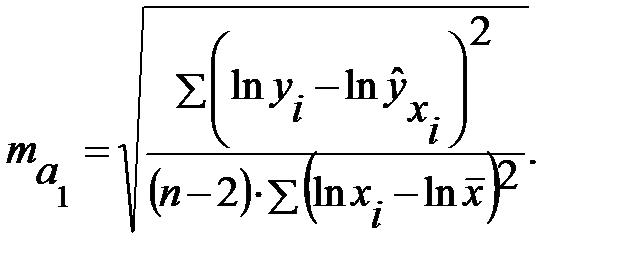 (2.28)
(2.28)
4.7. Множественный регрессионный анализ
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной 7 от нескольких объясняющих переменных 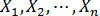 . Эта задача решается с помощью множественного регрессионного анализа.
. Эта задача решается с помощью множественного регрессионного анализа.
Обозначим 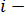 е наблюдение переменной
е наблюдение переменной 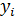 , а объясняющих переменных
, а объясняющих переменных 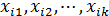 . Тогда модель множественной линейной регрессии можно представить в виде:
. Тогда модель множественной линейной регрессии можно представить в виде:
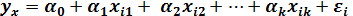 , (13.22)
, (13.22)
где 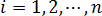 , а
, а 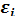 удовлетворяет приведенным выше предпосылкам (13.3)—(13.5).
удовлетворяет приведенным выше предпосылкам (13.3)—(13.5).
Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений. Матричное описание регрессии облегчает как теоретические концепции анализа, так и необходимые расчетные процедуры.
Введем обозначения: 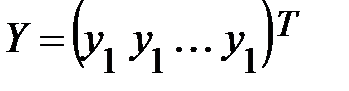 матрица-столбец, или вектор, значений зависимой переменной размера n;
матрица-столбец, или вектор, значений зависимой переменной размера n;
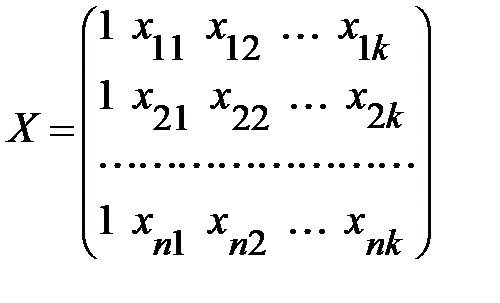
— матрица значений объясняющих переменных, или матрица плана размера (обращаем внимание на то, что в матрицу X дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что в модели (13.22) свободный член 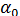 умножается на фиктивную переменную
умножается на фиктивную переменную 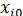 , принимающую значение 1 для всех
, принимающую значение 1 для всех 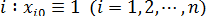 ;
;
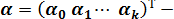 матрица-столбец, или вектор, параметров размера (k+1);
матрица-столбец, или вектор, параметров размера (k+1);
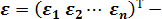 матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера п.
матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера п.
Тогда в матричной форме модель (13.22) примет вид:
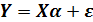 . (13.23)
. (13.23)
Оценкой этой модели по выборке является уравнение
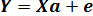 , (13.24)
, (13.24)
где 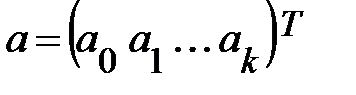 ,
, 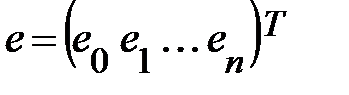 .
.
Для оценки вектора неизвестных параметров 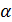 применим метод наименьших квадратов. Так как произведение транспонированной матрицы
применим метод наименьших квадратов. Так как произведение транспонированной матрицы 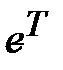 на саму матрицу
на саму матрицу 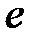
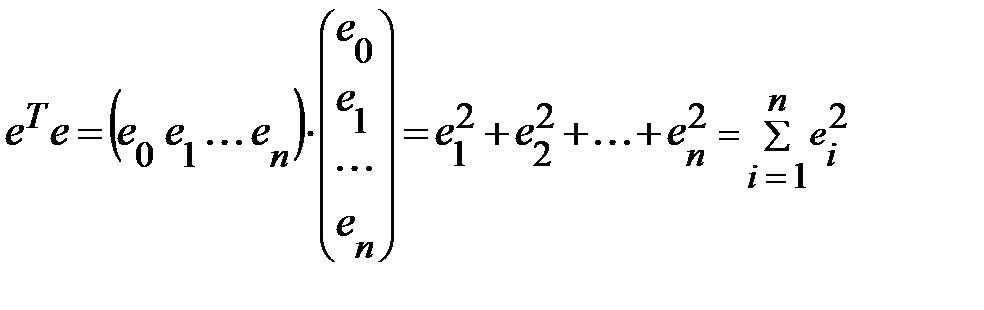 ,
,
то условие минимизации остаточной суммы квадратов запишется в виде:
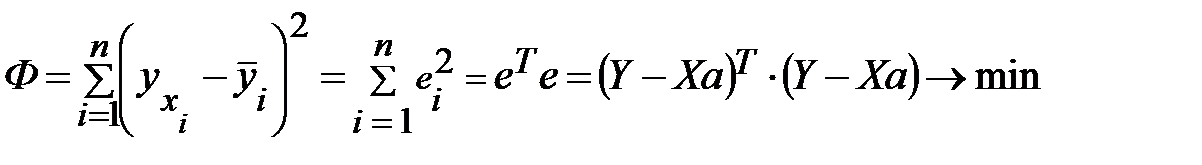 . (13.24)
. (13.24)
Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. 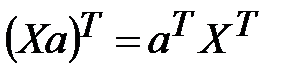 , получим после раскрытия скобок:
, получим после раскрытия скобок:
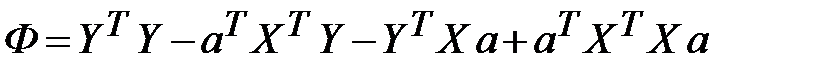 . (13.24)
. (13.24)
Произведение 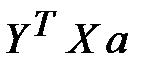 есть матрица размера
есть матрица размера 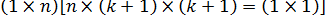 , т.е. величина скалярная, следовательно, оно не меняется при транспонировании:
, т.е. величина скалярная, следовательно, оно не меняется при транспонировании: 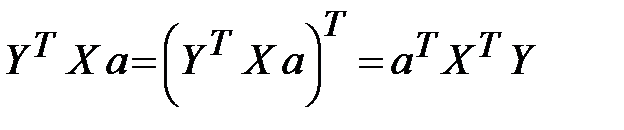 . Поэтому условие минимизации (13.24) примет вид:
. Поэтому условие минимизации (13.24) примет вид:
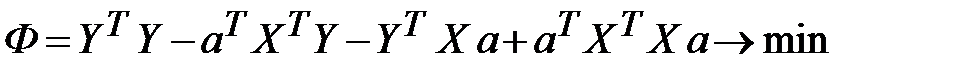 .
. 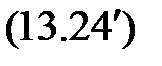
На основании необходимого условия экстремума функции нескольких переменных 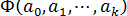 , представляющей
, представляющей 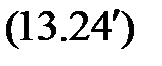 , необходимо приравнять к нулю частные производные по этим переменным или в матричной форме — вектор частных производных
, необходимо приравнять к нулю частные производные по этим переменным или в матричной форме — вектор частных производных
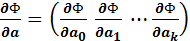 .
.
Таким образом, встает задача найти минимум этой функций. Для этого выражение 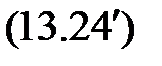 следует продифференцировать по векторному аргументу
следует продифференцировать по векторному аргументу 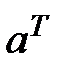 и полученное выражение приравнять к нулю, то есть:
и полученное выражение приравнять к нулю, то есть:

Отсюда получается следующее выражение:
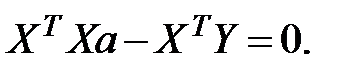
Данная система уравнений называется нормальной системой уравнений регрессии. Требуется ввести обозначения: 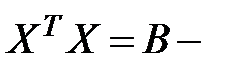 матрица коэффициентов нормальных уравнений,
матрица коэффициентов нормальных уравнений, 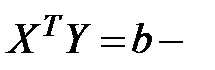 вектор-столбец свободных членов нормальных уравнений регрессии.
вектор-столбец свободных членов нормальных уравнений регрессии.
С учетом введенных обозначений нормальная система уравнений регрессии перепишется в окончательном виде:
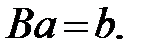 (13.25)
(13.25)
Для решения матричного уравнения (13.25) относительно вектора оценок параметров 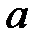 необходимо ввести предпосылку для множественного регрессионного анализа: матрица
необходимо ввести предпосылку для множественного регрессионного анализа: матрица 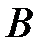 является неособенной, т.е. ее определитель не равен нулю. Следовательно, ранг матрицы
является неособенной, т.е. ее определитель не равен нулю. Следовательно, ранг матрицы 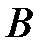 равен ее порядку, т.е.
равен ее порядку, т.е. 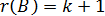 . Из матричной алгебры известно, что
. Из матричной алгебры известно, что 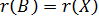 , значит,
, значит, 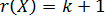 , т.е. ранг матрицы плана
, т.е. ранг матрицы плана 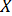 равен числу ее столбцов.
равен числу ее столбцов.
Кроме того, полагают, что число имеющихся наблюдений (значений) каждой из объясняющих переменных превосходит ранг матрицы 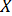 , т.е.
, т.е. 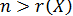 или
или 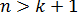 , ибо в противном случае в принципе невозможно получение сколько-нибудь надежных статистических выводов.
, ибо в противном случае в принципе невозможно получение сколько-нибудь надежных статистических выводов.
Если матрица коэффициентов нормальных уравнений 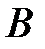 хорошо обусловлена и обратима, то можно получить решение системы (13.25), например, в виде:
хорошо обусловлена и обратима, то можно получить решение системы (13.25), например, в виде:
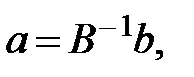 (13.26)
(13.26)
где 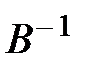 - обратная матрица, соответствующая условиям:
- обратная матрица, соответствующая условиям:
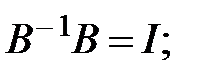
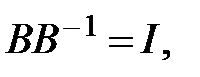
где 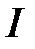 - единичная матрица соответствующих размеров.
- единичная матрица соответствующих размеров.
Зная вектор 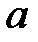 , модель уравнения множественной регрессии можно представить в виде:
, модель уравнения множественной регрессии можно представить в виде:
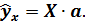 (13.27)
(13.27)
Преобразуем вектор оценок (13.26) с учетом (13.23) получим:
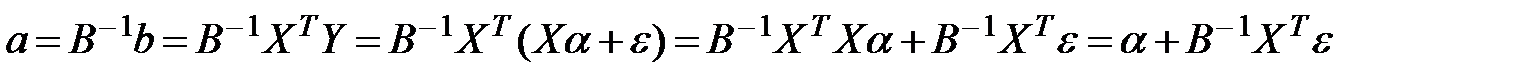 ,
,
Откуда
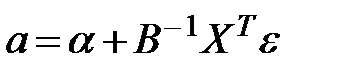 , (13.28)
, (13.28)
т. е. оценки параметров (13.28), найденные по выборке, будут содержать случайные ошибки.
Пример 13.4. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего Y(t), мощности пласта Х\ (м) и уровне механизации работ Х2 (%), характеризующие процесс добычи угля в 10 шахтах.
Таблица 13.6
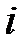 | 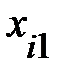 | 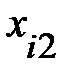 | 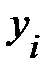 | 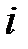 | 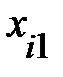 | 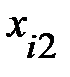 | 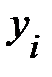 |
Предполагая, что между переменными 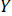 ,
, 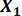 и
и 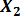 существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии
существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии 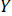 , по
, по 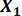 и
и 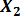 .
.
Решение. Обозначим
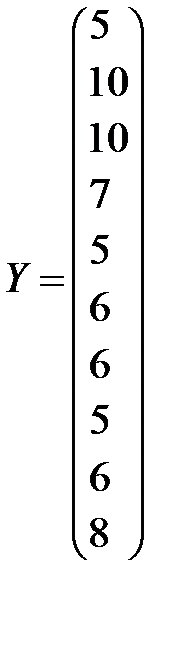 ,
, 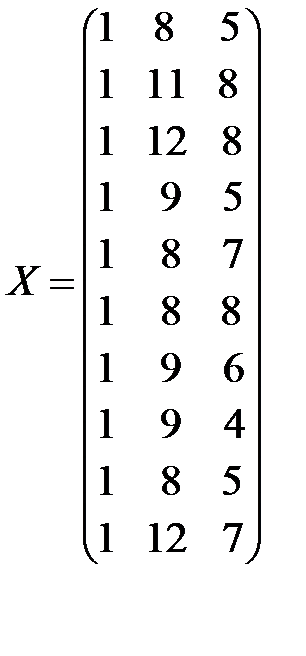

(напоминаем, что в матрицу плана X вводится дополнительный столбец чисел, состоящий из единиц).
Решение системы уравнении найдем методом псевдонормального решения:
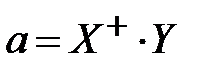 , (13.29)
, (13.29)
где 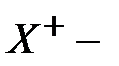 псевдообратная матрица к исходной матрице
псевдообратная матрица к исходной матрице 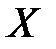 .
.
Псевдообратную матрицу найдем по рекурсивному алгоритму (№№№) и она равна:

Тогда по формуле (13.29) найдем вектор столбец параметров регрессии:
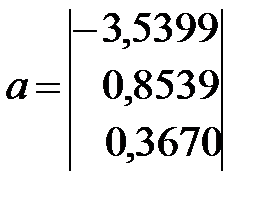 .
.
С учетом (13.27) уравнение множественной регрессии имеет вид:
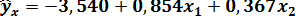 . (13.30)
. (13.30)
Уравнение множественной регрессии (13.30) показывает, что при увеличении только мощности пласта 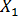 (при неизменном
(при неизменном 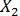 ) на 1 м, добыча угля на одного рабочего Y увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ
) на 1 м, добыча угля на одного рабочего Y увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ 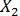 на 1% (при неизменной
на 1% (при неизменной 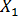 ) в среднем на 0,367 т.
) в среднем на 0,367 т.
Добавление в регрессионную модель новой объясняющей переменной 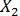 изменило коэффициент регрессии
изменило коэффициент регрессии 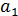 (Y по
(Y по 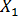 ) с 1,016 для парной регрессии (см. пример 13.1) до 0,854 — для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост зависимой переменной Y при изменении на единицу объясняющей переменной
) с 1,016 для парной регрессии (см. пример 13.1) до 0,854 — для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост зависимой переменной Y при изменении на единицу объясняющей переменной 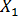 в чистом виде, независимо от
в чистом виде, независимо от 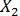 . В случае парной регрессии
. В случае парной регрессии 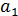 учитывает воздействие на Y не только переменной
учитывает воздействие на Y не только переменной 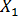 , но и косвенно корреляционно связанной с ней переменной
, но и косвенно корреляционно связанной с ней переменной 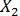 . ►
. ►
На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии 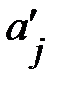 и коэффициенты эластичности
и коэффициенты эластичности 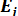 :
:
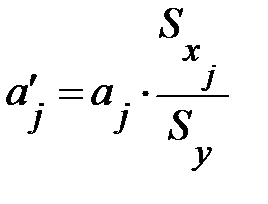 . (13.31)
. (13.31)
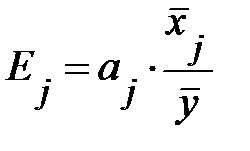 . (13.32)
. (13.32)
Стандартизованный коэффициент регрессии 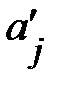 показывает, на сколько величин
показывает, на сколько величин 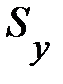 изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на
изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 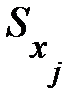 , а коэффициент эластичности
, а коэффициент эластичности 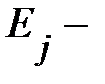 на сколько процентов (от средней) изменится в среднем Y при увеличении только
на сколько процентов (от средней) изменится в среднем Y при увеличении только 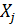 на 1%.
на 1%.
13.6. Ковариационная матрица и ее выборочная оценка
Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной:
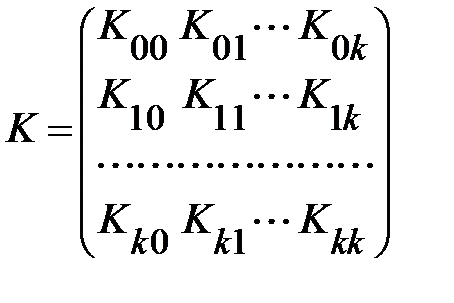 .
.
где элементы 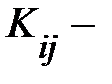 ковариации (или корреляционные моменты) оценок параметров
ковариации (или корреляционные моменты) оценок параметров 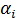 и
и 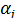
 . Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий (см. § 5.6). Поэтому
. Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий (см. § 5.6). Поэтому
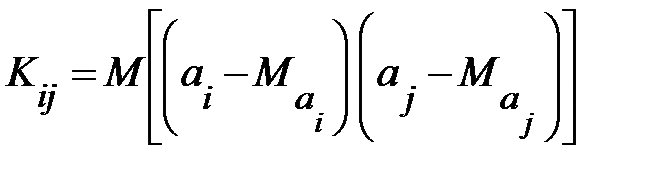 , (13.28)
, (13.28)
где 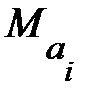 и
и 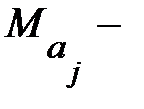 математические ожидания соответственно для параметров
математические ожидания соответственно для параметров 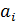 и
и 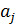 .
.
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
В силу того, что оценки 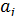 , полученные методом наименьших квадратов, являются несмещенными оценками параметров
, полученные методом наименьших квадратов, являются несмещенными оценками параметров 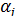 , т.е.
, т.е. 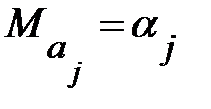 , выражение (13.28) примет вид:
, выражение (13.28) примет вид:
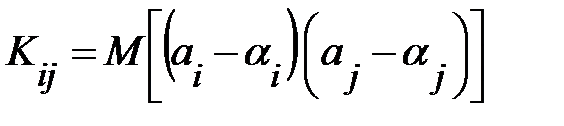 .
.
Рассматривая ковариационную матрицу К, легко заметить, что на ее главной диагонали находятся дисперсии опенок параметров регрессии, ибо
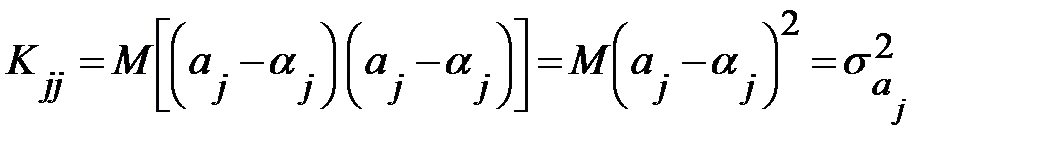 . (13.29)
. (13.29)
В сокращенном виде ковариационная матрица К имеет вид:
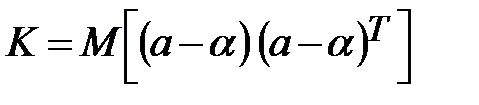 . (13.30)
. (13.30)
Учитывая (13.28) мы можем записать
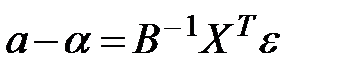 .
.
Тогда выражение (12.30) примет вид:
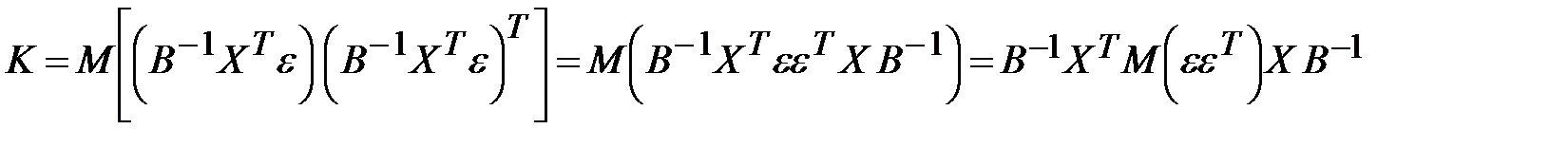 , (13.31)
, (13.31)
ибо элементы матрицы X —неслучайные величины.
Матрица 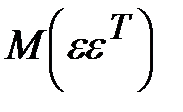 представляет собой ковариационную матрицу вектора возмущений
представляет собой ковариационную матрицу вектора возмущений 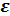 :
:
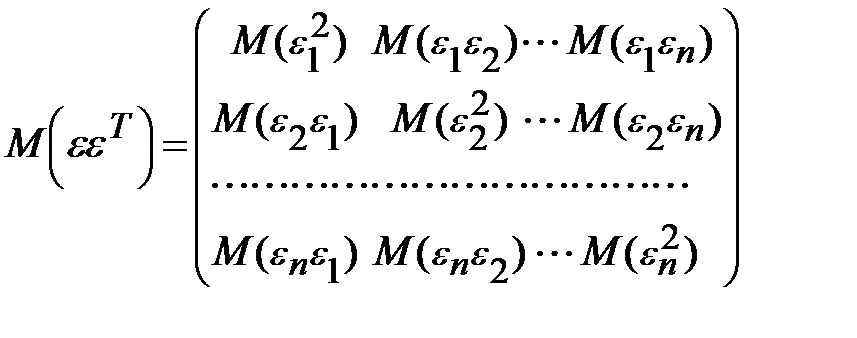
в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки 4 о некоррелированности возмущений 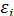 , и
, и 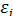 между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок 2 и 3 регрессионного анализа равны одной и той же дисперсии
между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок 2 и 3 регрессионного анализа равны одной и той же дисперсии 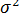 :
:
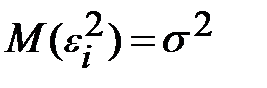 .
.
Поэтому матрица 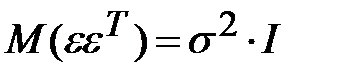 , где
, где 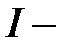 единичная матрица
единичная матрица 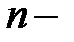 го
го
порядка. Следовательно, в силу (13.31) ковариационная матрица вектора 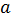 оценок параметров:
оценок параметров:
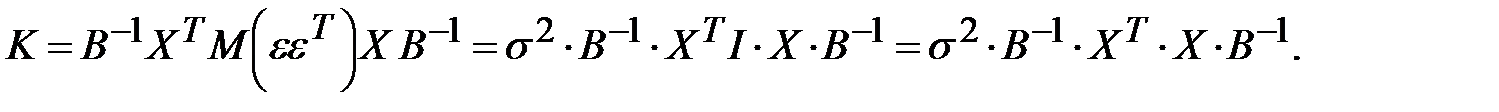
Так как 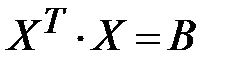 и
и 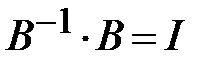 , то окончательно получим:
, то окончательно получим:
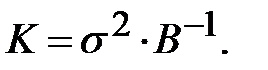 (13.32)
(13.32)
Таким образом, с помощью обратной матрицы 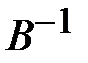 нормальных уравнении регрессииопределяется не только сам вектор
нормальных уравнении регрессииопределяется не только сам вектор 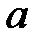 оценок параметров (13.28), но и дисперсии и ковариации его компонент.
оценок параметров (13.28), но и дисперсии и ковариации его компонент.
Входящая в (13.32) дисперсия возмущений неизвестна. Заменив ее выборочной остаточной дисперсией
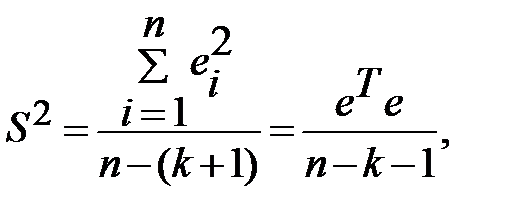 (13.33)
(13.33)
по (13.32) получаем выборочную оценку ковариационной матрицы К. (В знаменателе выражения (13.33) стоит 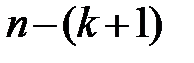 , а не
, а не 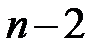 , как это было выше в (13.6). Это связано с тем, что теперь
, как это было выше в (13.6). Это связано с тем, что теперь 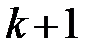 степеней свободы (а не две) теряются при определении неизвестных параметров, число которых вместе со свободным членом
степеней свободы (а не две) теряются при определении неизвестных параметров, число которых вместе со свободным членом 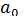 равно
равно 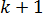 .
.
13.7. Определение доверительных интервалов
для коэффициентов и функции регрессии
Перейдем теперь к оценке значимости коэффициентов регрессии 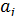 и построению доверительного интервала для параметров регрессионной модели
и построению доверительного интервала для параметров регрессионной модели 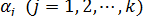 .
.
В силу (13.29), (13.32) и изложенного выше оценка дисперсии коэффициента регрессии 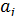 определится по формуле:
определится по формуле:
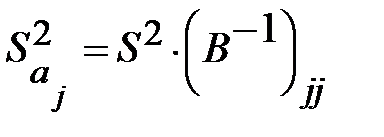
где 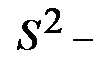 несмещенная оценка параметра
несмещенная оценка параметра
 2015-05-18
2015-05-18 2155
2155