2015-05-18
1139
Восемь свойств сложения и умножения, установленных в геометрической модели, позволяют построить арифметическую модель и называются аксиомами векторного пространства.
Рассмотрим примеры моделей, удовлетворяющих этим аксиомам.
Пример 1.
Множество многочленов степени не выше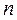 
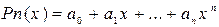
образует векторное пространство, в котором мономы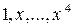 
– базисные элементы, а коэффициенты многочлена 
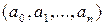– координаты вектора 
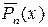в этом базисе.
