1. Для всякой фиксированной точки A0 Îe3 и произвольной точки B Îe3 отображение 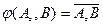
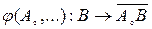 (1)
(1)
является взаимно-однозначным отображением точек B Îe3 на множество векторов  .
.
2.
 (Аксиома треугольников). Для любых трех точек A,B,C Îe3 справедливо равенство
(Аксиома треугольников). Для любых трех точек A,B,C Îe3 справедливо равенство 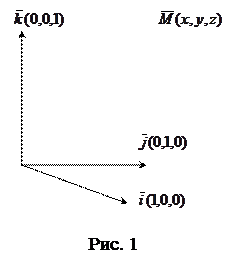
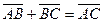 .
.
3. (Аксиома реализуемости операции откладывания). Существует хотя бы одна точка 0Îe3, для которой определена операция откладывания вектора 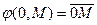 для любой точки
для любой точки 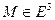 .
.
Точку 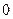 в аксиоме 3 называют началом координат в евклидовом пространстве e3, а вектор
в аксиоме 3 называют началом координат в евклидовом пространстве e3, а вектор 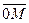 – радиус-вектором точки
– радиус-вектором точки 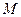 в этом пространстве. Координатами
в этом пространстве. Координатами 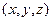 точки M Îe3 называют координаты радиус-вектора
точки M Îe3 называют координаты радиус-вектора 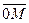 (рис.1) где
(рис.1) где 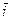 ,
, 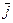 ,
, 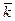 – направленные отрезки в e3, соответствующие базисным векторам
– направленные отрезки в e3, соответствующие базисным векторам 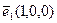 ,
, 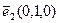 ,
, 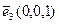 векторного пространства
векторного пространства 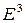 при отображении (1) с
при отображении (1) с 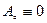 . Таким образом, по построению операции откладывания вектора в e3, приходим к векторному равенству
. Таким образом, по построению операции откладывания вектора в e3, приходим к векторному равенству
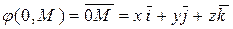 . (2)
. (2)
Это равенство, с учетом фиксированной точки 0Îe3, представляет взаимно-однозначное соответствие между точками M Îe3 и арифметически упорядоченными тройками чисел 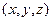 и является определяющим равенством для координат точек евклидова пространства.
и является определяющим равенством для координат точек евклидова пространства.
Для вычисления длин отрезков и углов между ними воспользуемся свойствами скалярного произведения (4), (6), (7), (8) из §3, а также свойством 1 операции откладывания отрезка.
Пусть требуется найти длину отрезка 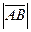 , если заданы координаты его концов
, если заданы координаты его концов 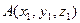 и
и 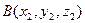 . Учитывая, что
. Учитывая, что 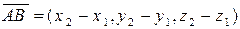 , из формулы (8) § 3 находим длину
, из формулы (8) § 3 находим длину
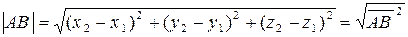 (3)
(3)
Пусть 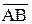 =
= 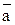 (u1,v1,w1) и
(u1,v1,w1) и 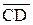 =
= 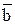 (u2,v2,w2) - направленные отрезки в e3 и пусть их координаты
(u2,v2,w2) - направленные отрезки в e3 и пусть их координаты 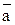 (u1,v1,w1)
(u1,v1,w1) 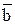 (u1,v1,w1) в Е3. Тогда, используя формулы (4), (7) и (8) из §3, получаем формулу для косинуса угла между
(u1,v1,w1) в Е3. Тогда, используя формулы (4), (7) и (8) из §3, получаем формулу для косинуса угла между 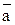 и
и 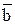
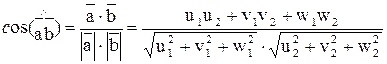 (4)
(4)
 2015-05-18
2015-05-18 1193
1193
