Использование множества значений функции

Иногда при решении уравнений полезно сравнить множество значений функций, находящихся в левой и правой частях уравнения.

Пример 1. Решить уравнение.

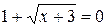
Решение. Область определения уравнения [-3; +∞). Поскольку функция y = 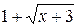, D(y) = [-3; +∞) может принимать только значения не меньше 1, а в правой части 0, то уравнение решений не имеет.

Ответ: решений нет.

Пример 2. Доказать, что уравнение

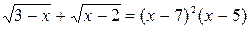
не имеет решений.

Решение. Найдем область определения функции f(x) = :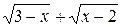

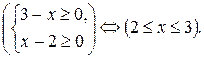
Итак, D(f) = [2; 3] и легко показать, что функция f(x) принимает только положительные значения. Но при 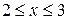функция g(x) = 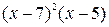принимает только отрицательные значения, поэтому, уравнение f(x) = g(x) решений не имеет, следовательно, решений не имеет и данное уравнение, что и требовалось доказать.