Исследование промежутков знакопостоянства функции

Напомним, что числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной, либо отрицательной), называют промежутками знакопостоянства. Это свойство иногда используют в теории уравнений.

Пример. Доказать, что уравнение

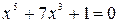
не имеет положительных корней.

Доказательство. Если x >0, то 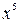>0, 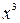>0 и тогда 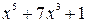> 0 и, следовательно, положительных корней уравнение не имеет.

Пример. Найти все целые значения параметра a, при которых уравнение

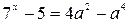
имеет корни.

Решение. Имеем 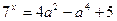. Так как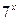 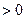, то данное уравнение имеет корни в зависимости от параметра a, если

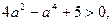
То есть 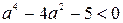. Решив это неравенство, получаем: 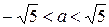. Выбираем целые значения a и получим: -2; -1; 0; 1; 2.

Ответ: при a равным -2; -1; 0; 1; 2 данное уравнение имеет корни.