2015-05-18
1588
Рассмотрим некоторые возможности применения этих свойств.
Иногда процесс решения уравнений значительно облегчается при применении следующего утверждения: если функцию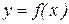 
— четная или нечетная, то корни уравнения 
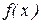= 0 (если они существуют) расположены на координатной прямой симметрично относительно точки 0, то есть если число x0 корень уравнения 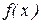= 0, то число - x0 также корень этого уравнения.
Пример. Решить уравнение.
.
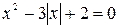Решение. Пусть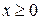 
, тогда получаем уравнение 
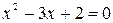, откуда 
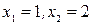. Поскольку функция 
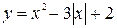— четная, то данное уравнение имеет отрицательные корни: 
.
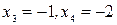Ответ: -1; -2; 1; 2.
В некоторых случаях предоставляется возможность воспользоваться таким утверждением: Если уравнение 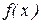= 0 имеет единственный корень x0 и 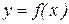— четная функция, то x0 = 0.
Пример. Найти все значения параметра a, при которых уравнение
,
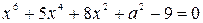Имеет ровно один действительный корень.
Решение. Рассмотрим функцию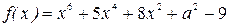 
, которая определена на множестве всех действительных чисел. Функция 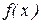является четной, а уравнение 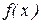= 0 по условию задачи должно иметь единственный корень, значит, x0 = 0.
|
|
|
Подставив это значение в исходное уравнение, получим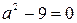 
, откуда 
.
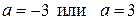Выполним проверку найденных значений параметра: если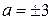 
, то уравнение 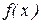= 0 принимает вид
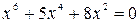, то есть 
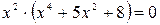, которое имеет ровно один корень x0 = 0.
