Классическая нормальная линейная модель наблюдений в условиях фиксированности значений объясняющих переменных

классическая нормальная линейная модель наблюдений

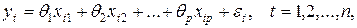
в которой предполагается, что значения объясняющих переменных 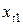, , 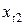…, , , 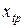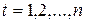фиксированы, а случайные составляющие 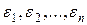(«ошибки») являются независимыми случайными величинами, имеющими одинаковое нормальное распределение с нулевым математическим ожиданием и конечной дисперсией (такие предположения об ошибках мы называем «стандартными».

Предположение о фиксированности значений объясняющих переменных в совокупности со стандартными предположениями об ошибках удобно с математической точки зрения: при таких предположениях оценки параметров, получаемые методом наименьших квадратов, имеют нормальное распределение, что, в свою очередь, дает возможность:

– строить доверительные интервалы для коэффициентов линейной модели, используя квантили 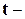распределения Стьюдента;

– проверять гипотезы о значениях отдельных коэффициентов, используя квантили 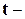распределения Стьюдента;

– проверять гипотезы о выполнении тех или иных линейных ограничений на коэффициенты модели используя квантили 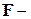распределения Фишера;

строить интервальные прогнозы для «будущих» значений объясняемой переменной, соответствующих заданным будущим значениям объясняющих переменных/

Вместе с тем, используемое в классической модели предположение о фиксированности значений объясняющих переменных в 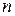наблюдениях означает, что имеет место возможность повторить наблюдения значений объясняемой переменной при том же наборе значений объясняющих переменных 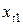, , 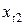…, , 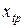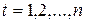; при этом получают другую реализацию (другой набор значений) случайных составляющих 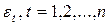, что приведет к значениям объясняемой переменной, отличающимся от значений 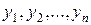, наблюдавшихся ранее.

С точки зрения моделирования реальных экономических явлений, предположение о фиксированности значений объясняющих переменных можно считать реалистическим лишь в отдельных ситуациях, связанных с проведением контролируемого эксперимента. Между тем в реальных ситуациях по большей части нет возможности сохранять неизменными значения объясняющих переменных. Более того, и сами наблюдаемые значения объясняющих переменных (как и «ошибки») часто интерпретируются как реализации некоторых случайных величин. В таких ситуациях становится проблематичным использование техники статистических выводов, разработанной для классической нормальной линейной модели.