С точки зрения моделирования реальных экономических явлений, предположение о фиксированности значений объясняющих переменных можно считать реалистическим лишь в отдельных ситуациях, связанных с проведением контролируемого эксперимента. Между тем в реальных ситуациях по большей части нет возможности сохранять неизменными значения объясняющих переменных. Более того, и сами наблюдаемые значения объясняющих переменных (как и «ошибки») часто интерпретируются как реализации некоторых случайных величин. В таких ситуациях становится проблематичным использование техники статистических выводов, разработанной для классической нормальной линейной модели.
Рассмотрим матрично-векторную форму записи классической линейной модели с 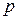 объясняющими переменными:
объясняющими переменными:
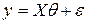 ,
,
в которой
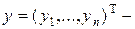 вектор значений объясняемой переменной в
вектор значений объясняемой переменной в 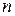 наблюдениях,
наблюдениях,
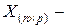 матрица значений объясняющих переменных в
матрица значений объясняющих переменных в 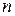 наблюдениях,
наблюдениях,  ,
,
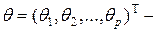 вектор коэффициентов,
вектор коэффициентов,
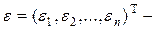 вектор случайных ошибок (возмущений) в п наблюдениях.
вектор случайных ошибок (возмущений) в п наблюдениях.
Если матрица 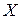 имеет полный ранг
имеет полный ранг 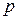 , то матрица
, то матрица 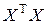 является невырожденной, для нее существует обратная матрица
является невырожденной, для нее существует обратная матрица 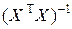 , и оценка наименьших квадратов для вектора
, и оценка наименьших квадратов для вектора 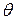 неизвестных коэффициентов имеет вид
неизвестных коэффициентов имеет вид
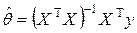 .
.
Математическое ожидание вектора оценок коэффициентов равно
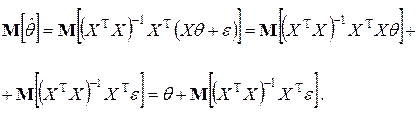
Если матрица 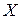 фиксирована, то
фиксирована, то 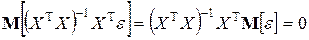 , так что:
, так что: 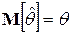 , т.е.
, т.е. 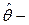 несмещенная оценка для
несмещенная оценка для 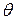 .
.
Если же мы имеем дело со стохастическими (случайными, недетерминированными) объясняющими переменными, то в общем случае 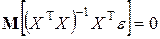 , так что
, так что 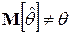 , и
, и 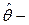 смещенная оценка для
смещенная оценка для 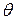 , и, кроме того, эта оценка уже не имеет нормального распределения.
, и, кроме того, эта оценка уже не имеет нормального распределения.
Если объясняющие переменные стохастические, то в некоторых случаях все же остается возможным использовать стандартную технику статистических выводов, предназначенную для классической нормальной линейной модели, по крайней мере, в асимптотическом плане (при большом количестве наблюдений).
13. Стандартная техника статистических выводов в условиях стохастичности переменных: ситуации А и А¢.
Если объясняющие переменные стохастические, то в некоторых случаях все же остается возможным использовать стандартную технику статистических выводов, предназначенную для классической нормальной линейной модели, по крайней мере, в асимптотическом плане (при большом количестве наблюдений).
В этом отношении наиболее благоприятной является:
Ситуация A
– случайная величина 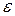 , не зависит (статистически) от
, не зависит (статистически) от 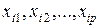 при всех
при всех 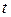 и
и 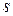 ,
,
– 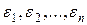 являются независимыми случайными величинами, имеющими одинаковое нормальное распределение с нулевым математическим ожиданием и конечной дисперсией
являются независимыми случайными величинами, имеющими одинаковое нормальное распределение с нулевым математическим ожиданием и конечной дисперсией 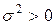 . (кратко будем обозначать это как
. (кратко будем обозначать это как 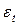 ~ i.i.d.
~ i.i.d. 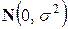 . Здесь i.i.d. – independent, identically distributed.)
. Здесь i.i.d. – independent, identically distributed.)
При выполнении таких условий имеем
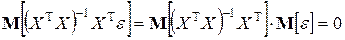 ,
,
так что оценка наименьших квадратов для  является несмещенной. Распределение статистик критериев («тестовых статистик») можно найти с помощью двухшаговой процедуры. На первом шаге находим условное распределение при фиксированном значении
является несмещенной. Распределение статистик критериев («тестовых статистик») можно найти с помощью двухшаговой процедуры. На первом шаге находим условное распределение при фиксированном значении  ; при этом значения объясняющих переменных рассматриваются как детерминированные (как в классической модели). На втором шаге получаем безусловное распределение соответствующей статистики, умножая условное распределение на плотность
; при этом значения объясняющих переменных рассматриваются как детерминированные (как в классической модели). На втором шаге получаем безусловное распределение соответствующей статистики, умножая условное распределение на плотность 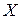 и интегрируя по всем возможным значениям
и интегрируя по всем возможным значениям 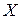 .
.
Если применить такую процедуру для получения безусловного распределения оценки наименьших квадратов 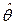 , то на первом шаге находим:
, то на первом шаге находим:
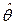 ~
~ 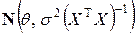 .
.
Интегрирование на втором этапе приводит к распределению, являющемуся смесью нормальных распределений 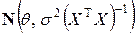 по
по  . Это распределение, в отличие от классического случая, не является нормальным.
. Это распределение, в отличие от классического случая, не является нормальным.
В то же время, для оценки  го коэффициента имеем:
го коэффициента имеем:
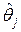 ~
~ 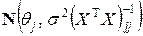
где 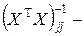
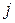 '-й диагональный элемент матрицы
'-й диагональный элемент матрицы 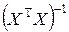 , так что
, так что
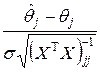 ~
~ 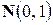 .
.
Условным распределением отношения 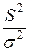 , где
, где 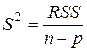 ,
, 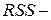 остаточная сумма квадратов, является
остаточная сумма квадратов, является 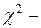 распределение с
распределение с 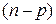 степенями свободы,
степенями свободы,
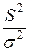 ~
~ 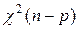 .
.
Заметим теперь, что 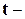 статистика для проверки гипотезы
статистика для проверки гипотезы 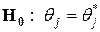 определяется соотношением
определяется соотношением
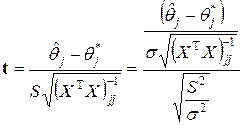 .
.
Из предыдущего вытекает, что если гипотеза 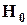 верна, то условное распределение этой
верна, то условное распределение этой 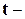 статистики имеет
статистики имеет 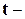 распределение Стьюдента с
распределение Стьюдента с 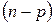 степенями свободы,
степенями свободы, 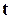 ~
~ 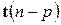 .
.
Это условное распределение одно и то же для всех X. Поэтому вне зависимости от того, какое именно распределение имеет 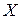 , безусловным распределением
, безусловным распределением 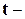 статистики для
статистики для 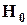 :
: 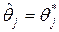 при выполнении этой гипотезы будет все то же распределение
при выполнении этой гипотезы будет все то же распределение 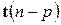 .
.
Аналогичное рассмотрение показывает возможность использования стандартных 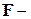 критериев для проверки линейных гипотез о значениях коэффициентов.
критериев для проверки линейных гипотез о значениях коэффициентов.
Те же самые выводы остаются в силе при замене предположений ситуации A следующим предположением.
Ситуация A'
– 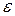 ~
~ 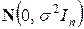 , где
, где 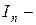 единичная матрица (размерности
единичная матрица (размерности  ). Для краткости будем далее обозначать:
). Для краткости будем далее обозначать: 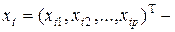 вектор значений
вектор значений 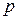 объясняющих переменных в
объясняющих переменных в 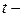 м наблюдении.
м наблюдении.
 2015-05-18
2015-05-18 641
641








