Сравнение центров распределения нормальных генеральных совокупностей

На практике иногда оказывается, что средний результат одной серии наблюдений заметно отличается от среднего результата другой серии.

Итак, имеем две случайные величины Х и Y. Обе подчиняются нормальному закону распределения. Допустим, что мы располагаем двумя независимыми выборками объемами n ₁ и n ₂ соответственно. Нулевая гипотеза: 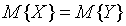. За альтернативную гипотезу примем 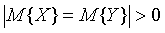. Дисперсии этих двух выборок будем считать известными.

Если гипотеза Н ₀ справедлива, то разность их арифметических средних 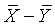распределена также по нормальному закону, а дисперсия этой разности (при условии, что Х и Y – независимы!) равна сумме дисперсий этих случайных переменных:

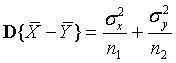Введем нормированную случайную величину 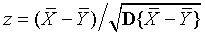, которая также распределена нормально и имеет дисперсию? равную единице, и математическое ожидание, равное нулю. С помощью таблицы, функции Лапласа, нетрудно установить критическое значение для | z |, которое наша разность не может превосходить с заданной вероятностью 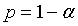. Если гипотеза H ₀ имеет место, то эта вероятность мало отличается от единицы. Чем меньше 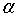, тем меньше вероятность отклонить проверяемую гипотезу.

Проверка гипотез о законе распределения. Критерий согласия .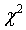

Существует несколько критериев согласия для проверки законов распределения случайной величины. Это критерии Колмогорова, Смирнова, 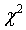Пирсона и др. Мы остановимся лишь на критерии Пирсона – это наиболее часто употребляемый критерий для проверки закона распределения случайной величины.

Сначала нужно разбить всю область изменения случайной величины на l интервалов (бин). Затем нужно подсчитать сколько этих величин попадает в каждый бин, то есть подсчитать эмпирические частоты т _к. Чтобы вычислить теоретические частоты нужно вероятность попадания в каждый бин р _к умножить на объем выборки n. Таким образом, статистика

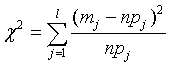является случайной величиной, подчиняющейся закону 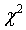с 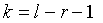степенями свободы. В последней формуле r – число параметров распределения, определяемых по выборке. Для нормального закона – это два параметра, для закона Пуассона – один и т.д.

Рассчитав значения 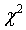и выбрав уровень значимости 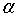, по таблице 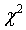- распределения определяют 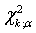. Если 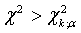, то гипотезу Н ₀ отвергают, если 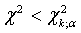то гипотезу принимают.