Постановка задачи
Под статистической гипотезой понимают всякое высказывание о генеральной совокупности, которое можно проверить по выборке. Как правило, статистические гипотезы делят на гипотезы о законах распределения и гипотезы о параметрах распределения.
Пусть 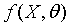 - закон распределения случайной величины Х, зависящий от одного параметра
- закон распределения случайной величины Х, зависящий от одного параметра 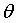 . Предположим, что наша гипотеза состоит в утверждении, что
. Предположим, что наша гипотеза состоит в утверждении, что 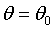 . Назовем эту гипотезу нулевой и обозначим ее H 0. Альтернативной, или конкурирующей гипотезой, которую обозначим H 1, будет
. Назовем эту гипотезу нулевой и обозначим ее H 0. Альтернативной, или конкурирующей гипотезой, которую обозначим H 1, будет 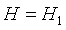 . Перед нами стоит задача проверки гипотезы Н 0 относительно конкурирующей гипотезы Н 1 на основании выборки, состоящей из n независимых наблюдений X 1, X 2, …, Xn. Следовательно, все возможное множество выборок объема n можно разделить на два непересекающихся подмножества (О и W) таких, что проверяемая гипотеза Н0 должна быть отвергнута, если наблюдаемая выборка попадает в подмножество W и принята, если выборка принадлежит подмножеству О.
. Перед нами стоит задача проверки гипотезы Н 0 относительно конкурирующей гипотезы Н 1 на основании выборки, состоящей из n независимых наблюдений X 1, X 2, …, Xn. Следовательно, все возможное множество выборок объема n можно разделить на два непересекающихся подмножества (О и W) таких, что проверяемая гипотеза Н0 должна быть отвергнута, если наблюдаемая выборка попадает в подмножество W и принята, если выборка принадлежит подмножеству О.
Подмножество О называют областью допустимых значений, а подмножество W – критической областью. При формировании критической области возможны ошибки
Ошибка первого рода состоит в том, нулевая гипотеза отвергается, то есть принимается гипотеза Н 1, в то время как в действительности верна гипотеза Н 0.
Ошибка второго рода состоит в том, что принимается гипотеза Н 0, а в действительности верна гипотеза Н 1.
Для любой заданной критической области будем обозначать через 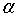 вероятность ошибки первого рода, а через
вероятность ошибки первого рода, а через 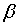 - вероятность ошибки второго рода. Следовательно, можно сказать, что при большом количестве выборок доля ложных заключений равна
- вероятность ошибки второго рода. Следовательно, можно сказать, что при большом количестве выборок доля ложных заключений равна 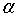 , если верна гипотеза H 0, и
, если верна гипотеза H 0, и 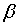 , если верна гипотеза H 1. При фиксированном объеме выборки выбор критической области W позволяет сделать как угодно малой либо
, если верна гипотеза H 1. При фиксированном объеме выборки выбор критической области W позволяет сделать как угодно малой либо 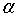 , либо
, либо 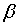 .
.
 2015-05-18
2015-05-18 344
344








