Непараметрические методы математической статистики - методы непосредственной оценки и проверки гипотез о теоретическом распределении вероятностей и тех или иных его общих свойствах (симметрии, независимости и т. п.) по результатам наблюдений. Особенность непараметрических методов в отличие от классических методов состоит в независимости от неизвестного теоретического распределения.
В качестве примера непараметрических можно привести критерий проверки согласованности теоретического и эмпирического распределений (критерий Колмогорова). Пусть результаты n независимых наблюдений имеют функцию распределения F(x) и пусть Fn(x) обозначает эмпирическую функцию распределения, построенную по n независимым наблюдениям (Fn - несмещённая и состоятельная оценка для F). Пусть Dn - наибольшее по абсолютной величине значение разности Fn(x) - F(x). Случайная величина √n•Dn имеет, в случае непрерывности F(x), функцию распределения Kn(λ), не зависящую от F(x) и стремящуюся при безграничном возрастании n к пределу
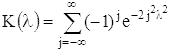
Отсюда при достаточно больших n для вероятности pn,λ неравенства √n•Dn ≥ λ получается приближённое выражение pn,λ ≈ 1 - K(λ). (*)
Функция K(λ) табулирована. Её значения для некоторых λ приведены в таблице.
| Таблица значений функции K(λ) | ||||||
| λ | 0.57 | 0.71 | 0.83 | 1.02 | 1.36 | 1.63 |
| K(λ) | 0.10 | 0.30 | 0.50 | 0.75 | 0.95 | 0.99 |
Равенство (*) используется для проверки гипотезы о том, что теоретическим распределением является распределение с заданной непрерывной функцией распределения F(x): сначала по результатам наблюдений находят значение величины Dn, а затем по формуле (*) вычисляют вероятность получить отклонение Fn от F, большее или равное наблюдённому. Если указанная вероятность достаточно мала, точнее равна наперёд заданному малому числу α, 0 < α < 1, то в соответствии с общими принципами проверки статистических гипотез проверяемую гипотезу отвергают. В противном случае считают, что результаты опыта не противоречат проверяемой гипотезе. Аналогично проверяется гипотеза о том, что две независимые выборки объёма n1 и n2 соответственно получены из одной и той же генеральной совокупности с непрерывным законом распределения, то есть что соответствующие функции распределения одинаковы (гипотеза однородности двух выборок). При этом вместо формулы (*) пользуются тем, что вероятность неравенства
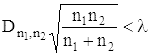
имеет пределом K(λ), где Dn1,n2 есть наибольшее по абсолютной величине значение разности Fn1(x) - Fn2(x). Приведённые примеры относятся к непараметрическим методам, основанным на разностях теоретической и эмпирической или двух эмпирических распределений
Дополнительным примером непараметрических методов могут служить методы проверки гипотезы о том, что теоретическое распределение принадлежит семейству нормальных распределений. Один из этих методов - так называемый метод выпрямленной диаграммы. Этот метод основывается на следующем замечании. Если случайная величина имеет нормальное распределение с параметрами a и σ, то
Φ-1[F(x)] = (x-a)/σ,
где Φ-1 - функция, обратная нормальной:
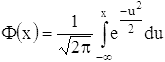
Таким образом, график функции y = Φ-1[F(x)] будет прямой линией, а график функции y = Φ-1[Fn(x)] - ломаной линией, близкой к этой прямой (рис.). Степень близости и служит простейшим критерием для проверки гипотезы нормальности распределения F(x).
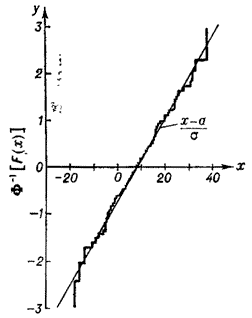 |
| Метод выпрямленной диаграммы |
Значительное место в современной математической статистике занимают непараметрические методы, в которых используются не сами эмпирические функции распределения, а некоторые функции от порядковых статистик - членов вариационного ряда. Если используются порядковые номера результатов наблюдений или ранги, то такие непараметрические критерии называют ранговыми, они, как правило, являются критериями однородности. Например, пусть X1,..., Xn и Y1,..., Ym - взаимно независимые элементы двух выборок с непрерывными функциями распределений. Для проверки гипотезы о том, что соответствующие Xi и Yj функции распределения одинаковы, можно использовать ранговый критерий, основанный на значениях функций от рангов: W = s(r1) +... + s(rm), где rj - ранг случайных величин Yj в общем вариационном ряду Xi и Yj, а функция s(r), r = l,..., n+m, определяется заранее заданной подстановкой
| ... | n+m | ||
| s(1) | s(2) | ... | s(n+m) |
где s(l),..., s(n+m) - одна из возможных перестановок чисел 1, 2,..., n+m. Выбор подстановки может быть осуществлён оптимальным образом.
 2015-05-18
2015-05-18 1148
1148








