Для интервальной оценки параметра мы использовали среднюю квадратическую погрешность как меру точности. Однако уместно задать вопрос, насколько эта мера точности реально отражает стандартное отклонение, связанное с погрешностью? Иначе говоря, когда мы вычисляем оценку дисперсии погрешности по формуле
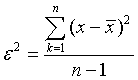 , ,
|
то необходимо знать и меру доверия этой величине. При небольших n эта оценка может значительно отличаться от точного значения дисперсии. Другими словами, нам нужно получить интервальную оценку дисперсии.
Известно, что величина 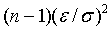 распределена по закону
распределена по закону 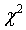 , которым и нужно воспользоваться для построения доверительного интервала. Этот закон не симметричный, поэтому нужно определять левую и правую границы отдельно. Допустим, что доверительная вероятность равна
, которым и нужно воспользоваться для построения доверительного интервала. Этот закон не симметричный, поэтому нужно определять левую и правую границы отдельно. Допустим, что доверительная вероятность равна 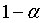 . Тогда вероятность того, что величина
. Тогда вероятность того, что величина 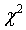 будет лежать правее левой границы доверительного интервала можно взять равной
будет лежать правее левой границы доверительного интервала можно взять равной 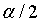 , а вероятность того, что она окажется больше правой границы, будет равна
, а вероятность того, что она окажется больше правой границы, будет равна 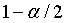 .
.
 2015-05-18
2015-05-18 701
701








