Пусть имеется 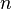 значений некоторой переменной
значений некоторой переменной 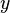 (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных
(это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных 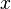 . Задача заключается в том, чтобы взаимосвязь между
. Задача заключается в том, чтобы взаимосвязь между 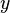 и
и 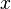 аппроксимировать некоторой функцией
аппроксимировать некоторой функцией 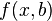 , известной с точностью до некоторых неизвестных параметров
, известной с точностью до некоторых неизвестных параметров 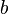 , то есть фактически найти наилучшие значения параметров
, то есть фактически найти наилучшие значения параметров 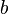 , максимально приближающие значения
, максимально приближающие значения 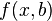 к фактическим значениям
к фактическим значениям 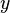 . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно
. Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно 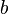 :
:
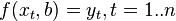
В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными
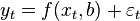
где 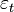 — так называемые случайные ошибки модели.
— так называемые случайные ошибки модели.
Соответственно, отклонения наблюдаемых значений 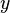 от модельных
от модельных 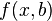 предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры
предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры 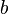 , при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии)
, при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) 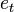 будет минимальной.
будет минимальной.
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК.Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки, продифференцировав её по неизвестным параметрам 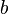 , приравняв производные к нулю и решив полученную систему уравнений:
, приравняв производные к нулю и решив полученную систему уравнений:
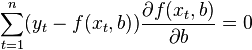
 2015-05-18
2015-05-18 558
558








