Метод наименьших квадратов в многомерном случае, его геометрическая интерпретация

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных.

Суть метода наименьших квадратов (МНК).

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 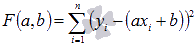принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

Уравнение множественной линейной регрессии.

Линейная модель множественной регрессии выглядит следующим образом:

Y = β0 + β1x1 + β2x2 + …+ βkxk + ε,

где Y – зависимая переменная (результативный признак);

x1,…,xk – независимые, или объясняющие переменные;

b0, b1,…, bk – коэффициенты регрессии;

e – ошибка регрессии.

2