При наличии тенденции значение каждого последующего уровня ряда зависит от предыдущих значений. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями yt исходного времен- ного ряда и уровнями 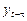 этого ряда, сдвинутыми на t шагов во времени, по следующей формуле: этого ряда, сдвинутыми на t шагов во времени, по следующей формуле: 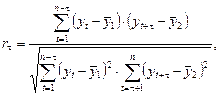 где где 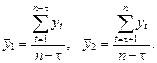 Число периодов Число периодов 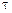 , по которым рассчитывается коэффициент автокорреляции, называется лагом. Считается целесообразным для обеспечения статистической достоверности коэф- фициентов автокорреляции использовать правило: максимальный лаг должен быть не больше n/4. Коэффициент автокорреляции является аналогом линейного коэффициента корреляции, изменяется в пределах от –1 до 1. Его значимость оценивается с помощью t -статистики: , по которым рассчитывается коэффициент автокорреляции, называется лагом. Считается целесообразным для обеспечения статистической достоверности коэф- фициентов автокорреляции использовать правило: максимальный лаг должен быть не больше n/4. Коэффициент автокорреляции является аналогом линейного коэффициента корреляции, изменяется в пределах от –1 до 1. Его значимость оценивается с помощью t -статистики: 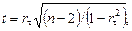 которая имеет распределение Стьюдента с которая имеет распределение Стьюдента с 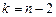 степенями свободы. Если степенями свободы. Если 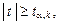 то проверяемый коэффициент значим. На основании автокорреляционных коэффициентов осуществляется анализ структуры временного ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только трендовую и случайную компоненты. Если наиболее высоким оказался коэффициент автокорреляции порядка t, то ряд содержит циклические колебания с периодичностью t. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать предположение относительно структуры этого ряда: ряд не содержит тренда и циклических колебаний, а только случайную компоненту. По коэффициенту автокорреляции можно судить о наличии линейного тренда. Если временной ряд имеет сильную нелинейную тенденцию, то коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Последовательность коэффициентов автокорреляции уровней первого, второго и следующих порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой. При помощи ана- лиза автокорреляционной функции и коррелограммы можно выявить структуру ряда. то проверяемый коэффициент значим. На основании автокорреляционных коэффициентов осуществляется анализ структуры временного ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только трендовую и случайную компоненты. Если наиболее высоким оказался коэффициент автокорреляции порядка t, то ряд содержит циклические колебания с периодичностью t. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать предположение относительно структуры этого ряда: ряд не содержит тренда и циклических колебаний, а только случайную компоненту. По коэффициенту автокорреляции можно судить о наличии линейного тренда. Если временной ряд имеет сильную нелинейную тенденцию, то коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Последовательность коэффициентов автокорреляции уровней первого, второго и следующих порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой. При помощи ана- лиза автокорреляционной функции и коррелограммы можно выявить структуру ряда. |
Так как максимальным является коэффициент автокорреляции первого порядка (таблица 26 и рисунок 15), то исследуемый ряд не содержит сезонной компоненты, т. е. содержит только трендовую и случайную структурные компоненты.
Таблица 26 – Значения автокорреляционной функции
| Период | Коэф. автокор. |
| 0,99 | |
| 0,98 | |
| 0,98 | |
| 0,97 | |
| 0,97 |
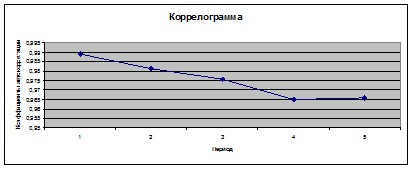
Рисунок 15 – Автокорреляционная функция
Так как все наблюдаемые значения t -статистики больше критического (таблица 27), то все коэффициенты автокорреляции значимы. Это подтверждает предположение о том, что ряд содержит трендовую и случайную компоненты.
Таблица 27 – Значимость коэффициентов автокорреляции
| Значимость | |
| t1 | 28,15 |
| t2 | 21,57 |
| t3 | 18,97 |
| t4 | 15,66 |
| t5 | 15,80 |
| tкр | 2,10 |
 2015-05-18
2015-05-18 1488
1488








