2015-05-18
1230
Задача 1. Имеются следующие показатели
| № | Страна | ВВП, млн. $ | Государственные расходы на образование, млн. $ |
| Швеция | 124,15 | 11,22 | |
| Швейцария | 101,65 | 5,31 | |
| Бельгия | 119,49 | 7,15 | |
| Мексика | 186,33 | 5,46 | |
| США | 2586,4 | 181,3 | |
| ФРГ | 38,62 | ||
| Италия | 395,52 | 15,95 | |
| Бразилия | 249,72 | 8,92 | |
| Франция | 655,29 | 33,59 | |
| Канада | 261,41 | 18,9 | |
| Австралия | 140,98 | 8,66 | |
| Саудовская Аравия | 115,97 | 6,4 | |
| Великобритания | 534,97 | 29,9 | |
| Испания | 211,78 | 4,79 | |
| Нидерланды | 169,38 | 13,41 | |
| Аргентина | 153,85 | 5,56 | |
| Япония | 1040,45 | 61,61 |
Задание: Проверьте предположение о наличии гетероскедастичности с помощью теста ранговой корреляции Спирмена, если зависимость между изучаемыми показателями выражается уравнением: y(x)=-2,32+0,067x; tтабл=2,13
Решение: Построим расчетную таблицу:
| ранг х | хi | yi | yxi | e I = 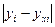 | ранг e | Di = ранг х -ранг e | (Di)2 |
| Итого |
Определим коэффициент ранговой корреляции Спирмена:
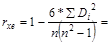
Определим расчетное значение t-критерия: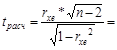 
Т.к. tрасч tтабл, то
Задача 2. По 20 наблюдениям была построена модель зависимости расходов на питание, ден. ед., у от доходов, ден. ед., х:
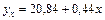
| № | х | остаток e i= 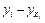 | Расчет ранговой корреляции | |||
| ранг х | ранг |e| | Di = ранг х -ранг e | (Di)2 | |||
| -12 | ||||||
| -11,7 | ||||||
| -5,4 | ||||||
| -5,6 | ||||||
| -2,8 | ||||||
| 0,8 | ||||||
| -1,6 | ||||||
| -4,0 | ||||||
| -6,2 | ||||||
| 6,6 | ||||||
| 13,7 | ||||||
| 12,2 | ||||||
| 4,4 | ||||||
| 4,0 | ||||||
| 3,4 | ||||||
| 23,2 | ||||||
| 16,2 | ||||||
| -16,8 | ||||||
| -27,8 | ||||||
| 9,8 | ||||||
| Σ |
Требуется:
1. Построить график остатков в зависимости от значений переменной х и сделать вывод.
2. Применить тест ранговой корреляции Спирмена для оценки гетероскедастичности.
3. Применить тест Гольдфельда-Квандта.
Решение:
1. График остатков имеет вид:
2. Проранжируем значения х и абсолютные величины е в порядке возрастания и найдём коэффициент ранговой корреляции Спирмена:
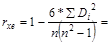
Найдём t -критерий для ранговой корреляции:
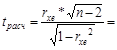
Сравним это значение с табличным при 5%-м уровне значимости и числе степеней свободы 18:
Т.к. tрасч tтабл, то
3. Для применения теста Гольдфельда-Квандта требуется информация об у. Хотя эти данные в условии не приведены, их можно найти. На основе уравнений регрессии 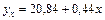найдём расчетные значения 
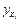. Далее найдём фактические значения 
.
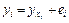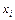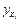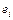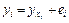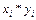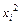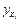| № |  | |  | |  |  | по группе | 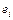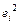по группе |  по группе |
| -12 | |||||||||
| -11,7 | |||||||||
| -5,4 | |||||||||
| -5,6 | |||||||||
| -2,8 | |||||||||
| 0,8 | |||||||||
| -1,6 | |||||||||
| -4,0 | |||||||||
| Σ | - | - | - | - | |||||
| -6,2 | |||||||||
| 6,6 | |||||||||
| 13,7 | |||||||||
| 12,2 | |||||||||
| 4,4 | |||||||||
| 4,0 | |||||||||
| 3,4 | |||||||||
| 23,2 | |||||||||
| 16,2 | |||||||||
| -16,8 | |||||||||
| -27,8 | |||||||||
| 9,8 | |||||||||
| Σ | - | - | - | - |
Исключив С центральных наблюдений, разобьём совокупность на две части: а) со значениями х ниже центральных; б) со значениями х выше центральных.
Пусть С=4, это наблюдения с порядковыми номерами 9-12. тогда в каждой части остаётся по 8 наблюдений. По каждой части находим уравнение регрессии.
Для первой группы:
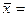
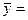
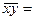
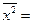
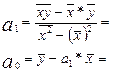
Тогда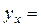 
Для второй группы:
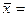
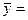
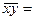
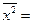
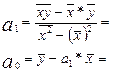
Тогда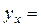
Для каждой группы определяем теоретические значения 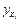, остатки 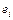и их квадраты .
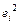Находим соотношение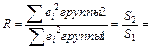 
Сравним эту величину с табличным значением F-критерия при 5%-м уровне значимости и числе степеней свободы 6 для каждой остаточной суммы квадратов.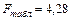 
Так как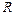 
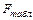, то
Задача 3. При изучении зависимости себестоимости единицы изделия (yi, тыс. руб.) от величины выпуска продукции (хi, тыс. руб.) по группам предприятий были получены следующие результаты: yxi = 2,12 – 0,11х
| ранг х | хi | yi | yxi | Е i= 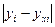| ранг Е | Di = ранг х-ранг Е | (Di)2 |
| 1,9 | |||||||
| 1,7 | |||||||
| 1,8 | |||||||
| 1,6 | |||||||
| 1,4 | |||||||
| Итого | 8,4 |
Задание: Проверьте предположение о наличии гетероскедастичности с помощью теста ранговой корреляции Спирмена, если зависимость между изучаемыми показателями выражается уравнением: yxi = 2,12 – 0,11х; tтабл=3,182.
Решение:
Найдём коэффициент ранговой корреляции Спирмена:
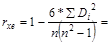
Найдём t -критерий для ранговой корреляции:
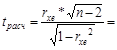
Сравним это значение с табличным при 5%-м уровне значимости и числе степеней свободы 18:
Т.к. tрасч tтабл, то
Задача 4. Имеются следующие данные:
| № р/на города | Поступление доходов в бюджет города, млрд. руб. | Численность работающих на крупных предприятиях, тыс. чел. |
| 28,8 | ||
| 15,5 | ||
| 12,9 | ||
| 4,4 | ||
| 90,5 | ||
| 132,4 | ||
| 114,2 | ||
| 37,5 | ||
| 88,3 | ||
| 99,1 | ||
| 209,5 | ||
| 48,7 | ||
| 8,1 | ||
| 150,6 | ||
| 342,9 | ||
| 156,1 | ||
| 104,6 | ||
| 20,8 | ||
| 68,6 |
Задание: проверьте предположение о наличие гетероскедостичности с помощью теста Гольдфельда-Квандта, если Fтабл=4,28; кол-во центральных наблюдений с=4
Решение: построим расчетную таблицу:
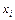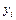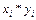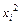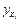| № | |  | | | по группе | 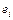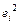по группе | по группе |
| Σ | - | - | |||||
| Σ | - | - |
Исключив С центральных наблюдений, разобьём совокупность на две части: а) со значениями х ниже центральных; б) со значениями х выше центральных.
Пусть С=4, это наблюдения с порядковыми номерами 9-12. тогда в каждой части остаётся по 8 наблюдений. По каждой части находим уравнение регрессии.
Для первой группы:
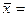
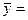
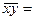
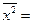
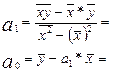
Тогда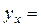
Для второй группы:
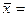
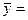
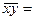
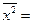
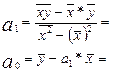
Тогда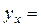
Для каждой группы определяем теоретические значения 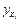, остатки 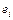и их квадраты .
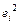Находим соотношение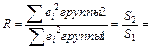
Сравним эту величину с табличным значением F-критерия при 5%-м уровне значимости и числе степеней свободы 6 для каждой остаточной суммы квадратов.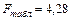
Так как 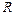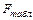, то
