МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
ЭКОНОМИКИ И ТОРГОВЛИ
С.В.Дёминова

Студента (ки) группы____________
ФИО______________________________
ОРЕЛ - 2013
Тема 1: Парная регрессия и корреляция
Задача 1.
Фирма провела рекламную кампанию. Через 10 недель фирма решила проанализировать эффективность этого вида рекламы, сопоставив недельные объёмы продаж с расходами на рекламу:
| Номер региона | Недельные объёмы продаж, тыс. руб. | Расходы на рекламу, тыс. руб. |
Задание:
1. Постройте линейное уравнение парной регрессии у от х.
2. Рассчитайте линейный коэффициент парной корреляции
3. Рассчитайте коэффициент детерминации.
4. Определите среднюю ошибку аппроксимации.
5. Оцените статистическую значимость параметров регрессии и корреляции.
6. С вероятностью 0,95 оцените доверительный интервал ожидаемой величины недельного объёма продаж компании с уровнем расходов на рекламу в 13 тыс. руб.
|
|
|
Решение:
1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу:
| №п/п | 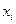 | 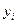 | 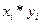 | 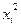 | 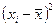 | 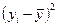 | 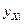 | 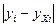 | 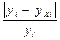 , (Аi%) , (Аi%) | 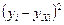 |
| Итого |
Рассчитаем промежуточные показатели:
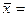
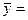
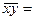
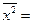
Рассчитаем параметры уравнения:
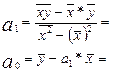
Получено следующее уравнение регрессии: 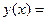
Коэффициент регрессии 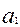 показывает, что
показывает, что
2. Тесноту линейной связи оценивает коэффициент корреляции. Для его определения рассчитаем следующие показатели:
Дисперсию факторного признака 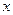 :
:
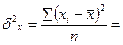
Среднее квадратическое отклонение факторного признака 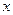
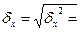
Дисперсию результативного признака 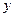
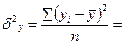
Среднее квадратическое отклонение результативного признака y
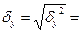
Далее рассчитаем коэффициент корреляции:
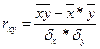
Так как rxy
3. Определим коэффициент детерминации:
D = 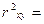
Он показывает, что вариация результативного признака 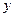 на ….% зависит от вариации факторного признака
на ….% зависит от вариации факторного признака 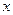
4. Качество модели оценим с помощью средней ошибки аппроксимации:
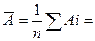
5. Оценку статистической значимости параметров регрессии проведем с помощью t-критерия Стьюдента.
Определим остаточную дисперсию:
|
|
|
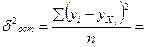
Определим случайные ошибки параметров уравнения и коэффициента корреляции:
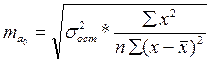
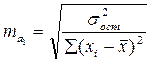
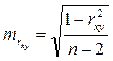
Определим расчетные значения t-критерия Стьюдента.
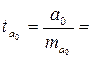
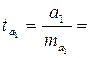
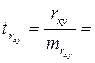
tтабл. при заданных степенях свободы df = n-2 = 10 – 2 = 8 и уровне значимости 5% (уровень надёжности 0,95 (95%)) составляет 2,306.
Сравним расчетные значения t-критерия Стьюдента с табличным:
6. Полученные оценки уравнения регрессии позволяют его использовать для прогнозирования. Предполагаемые расходы на рекламу на следующую неделю составят 13 тыс. руб., то есть 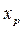 = 13 тыс. руб.
= 13 тыс. руб.
Тогда прогнозное значение недельных объёмов продаж составит:
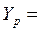
Ошибка прогноза составит:
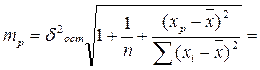
Предельная ошибка прогноза, которая в 95% не будет превышена, составит следующую величину:
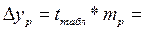
Построим доверительный интервал прогноза:
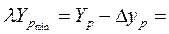
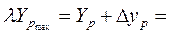
Выполненный прогноз показывает, что при уровне расходов на рекламу в 13 тыс. руб., недельный объём продаж фирмы будет находиться в пределах от …….. тыс. руб. до ……………. тыс. руб.
Задача 2. При исследовании корреляционной зависимости между ценой на нефть и индексом нефтяных компаний получены следующие данные:
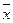 =16,2 (ден. ед.),
=16,2 (ден. ед.), 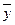 =4000 (усл. ед.), (
=4000 (усл. ед.), (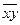 -
- 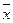 *
* 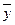 ) = 40,
) = 40, 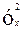 =4,
=4, 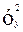 =500.
=500.
Задание:
1) составьте уравнение регрессии;
2) используя полученное уравнение регрессии, найдите среднее значение индекса при цене на нефть 16,5 ден. ед.
Решение:
Задача 3. Имеются следующие данные по семи территориям Уральского района
| Район | Расходы на покупку продовольственных товаров, % | Среднедневная заработная плата одного рабочего, у.е. |
| Удмуртия | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 58,8 | |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Задание:
1) для характеристики зависимости определите параметры функции равносторонней гиперболы
2) оцените полученную модель через среднюю ошибку аппроксимации и 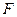 - критерий Фишера.
- критерий Фишера.
Решение:
1)уравнение равносторонней гиперболы
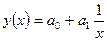 приводится к линейному виду при замене
приводится к линейному виду при замене 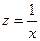 , тогда получим следующее уравнение:
, тогда получим следующее уравнение:
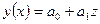
В соответствии с методом наименьших квадратов, параметры уравнения определяются по следующим формулам:
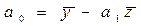
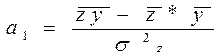
| № | 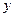 | 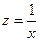 | zy | 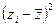 | 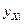 | 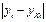 | 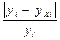 , (Аi%) , (Аi%) | 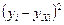 | 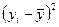 |
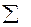 |
1) 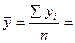
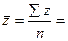
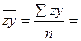
Определим дисперсию 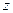
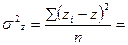
Определим параметры уравнения
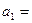
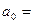
Уравнение регрессии имеет следующий вид:
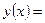
2) Определим среднюю ошибку аппроксимации
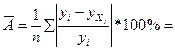
Оценим тесноту связи с помощью индекса корреляции
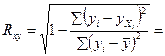
Оценим статистическую значимость уравнения регрессии с помощью 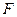 - критерия Фишера:
- критерия Фишера:
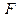 факт
факт 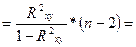
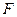 табл. при заданных степенях свободы
табл. при заданных степенях свободы 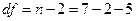 и уровне значимости
и уровне значимости 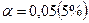 составляет 6,61.
составляет 6,61.
Таким образом,
Задача 4. Зависимость среднемесячной производительности труда о возраста рабочих характеризуется моделью: 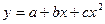 . Ее использование привело к следующим результатам:
. Ее использование привело к следующим результатам:
| № п/п | Производительность труда рабочих, тыс.руб. | № п/п | Производительность труда рабочих, тыс.руб., | ||
| фактическая | расчетная | фактическая | расчетная | ||
Задание: Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера.
Решение: построим расчетную таблицу:
| № п/п | 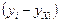 | 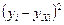 |
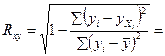
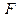 факт
факт 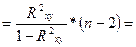
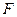 табл.=5,32
табл.=5,32
Задача 5. По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов:
| Признак - фактор | Уравнение парной регрессии | Среднее значение фактора |
| Объем производства млн.руб., х1 | 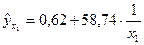 | 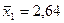 |
| Трудоемкость единицы продукции, чел.-час., х2 | 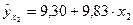 | 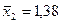 |
Задание: Определите с помощью коэффициентов эластичности силу влияния каждого фактора на результат.
|
|
|
Решение:
Для уравнения равносторонней гиперболы 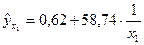 :
:
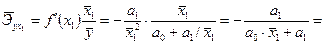
Для уравнения прямой 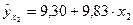 :
:
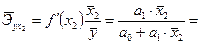
Задача 5. По территории центрального района известны следующие данные
| Район | Доля денежных доходов, направленных на сбережения, % | Среднемесячная заработная плата, у.е. |
| Брянская обл. | 6,9 | |
| Владимирская обл. | 8,7 | |
| Ивановская обл. | 3,4 | |
| Калужская обл. | 8,4 | |
| Костромская обл. | 6,1 | |
| Орловская обл. | 9,4 | |
| Рязанская обл. | 11,0 | |
| Смоленская обл. | 6,4 | |
| Тверская обл. | 9,3 | |
| Тульская обл. | 8,2 | |
| Ярославская обл. | 8,6 |
Задание:
1. Постройте линейное уравнение парной регрессии у от х.
2. Рассчитайте линейный коэффициент парной корреляции
3. Рассчитайте коэффициент детерминации.
4. Определите среднюю ошибку аппроксимации.
5. Оцените статистическую значимость параметров регрессии и корреляции (tтабл.)=2,26.
6. С вероятностью 0,95 оцените доверительный интервал ожидаемой доли денежных доходов, направленных на сбережения с уровнем среднемесячной заработной платы в 392 у.е.
 2015-05-18
2015-05-18 1591
1591