Уравнения звеньев

Система автоматического управления (САУ) – это совокупность соединенных в определенной последовательности элементов и устройств, которые будем называть звеньями. Примерами звеньев могут служить объекты управления, усилительно-преобразовательные устройства, исполнительные двигатели, тахогенераторы, различного рода датчики, цифровые устройства, в том числе микропроцессоры и управляющие ЭВМ и т.п.

Под линейной непрерывной стационарной системой с сосредоточенными параметрами будем понимать систему, которая в целом так же, как и отдельные звенья, описывается линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами.

На рис. 2.1 изображено звено САУ, имеющее один входной 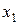и один
выходной 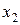сигналы, являющиеся скалярными величинами (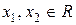, где
R – множество действительных или комплексных чисел). В дальнейшем будем интерпретировать все сигналы в системе как функции текущего времени t, т.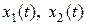е. , где .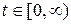

Рис. 2.1

Получение уравнений, описывающих поведение отдельных звеньев в каждом конкретном случае, является задачей той или иной отрасли науки, например, электротехники, электроники, механики и т.п. и не является предметом данного курса. Поэтому будем по-

лагать, что звено в общем случае описывается дифференциальным уравнением следующего вида:

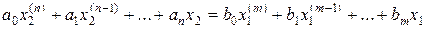, (2.1)

где ; .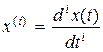

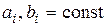Коэффициенты 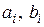зависят от конструктивных параметров и, возможно, от режима работы звена. Порядок n дифференциального уравнения (2.1) будет определять также и соответствующий порядок звена. На практике звенья описываются дифференциальными уравнениями низкого порядка, обычно .

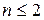Для полного математического описания процессов в звене следует задавать начальные условия 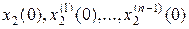, которые чаще всего будем полагать нулевыми.

В теории автоматического управления наряду с (2.1) уравнения звеньев записывают в стандартной форме, когда коэффициенты при переменных 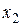и 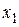равны единице. Вынося за скобк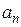и и 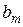, имеем

,

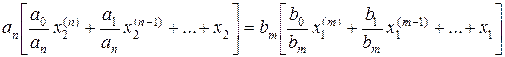или, вводя обозначения 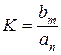, , 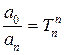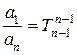…; 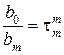, ,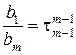…, получим следующий вид дифференциального уравнения:

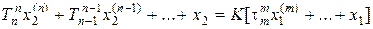, (2.2)

где 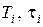– постоянные времeни, имеющие размерность [с], а K – коэффициент пepeдачи (усилeния) имеет размерность [разм. х ₂ / разм. х ₁].

Уравнения (2.1) и (2.2) можно записать также в операторном (символическом) виде, вводя дифференциальный оператор 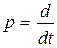такой, что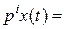 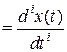. Тогда уравнение (2.1) может быть записано в операторной форме: 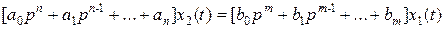. обозначая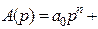 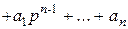, , 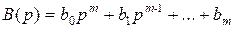будем иметь

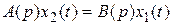. (2.3)

По виду дифференциального уравнения (2.1) звенья делятся на три типа. Есл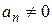и и 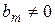, то такие звенья относятся к позиционным; если 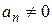, а 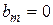, то к дифференцирующим;если 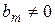, , 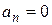то к интегрирующим.

Позиционные звенья имеют статичeскую хаpактepистику. Пусть х ₁ = const, х ₂ = const, тогда 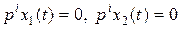и .

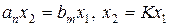Уравнения (2.1)–(2.3) описывают поведение звеньев в динамических режимах, поэтому в дальнейшем будем называть их уравнениями динамики.

Пример 2.1. Рассмотрим дифференциальные уравнения часто встречающихся звеньев САУ. В качестве исполнительного устройства в системах управления широко применяются двигатели. Дифференциальное уравнение динамики двигателя постоянного тока при якорном управлении при определенных условиях имеет вид

,

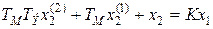где Т_м, Т_э – электромеханическая и электромагнитная постоянные времени;
K – коэффициент передачи; 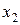– угловая скорость вращения; 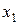– напряжение, приложенное кякорю.

Обозначая 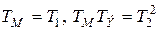, можно получить уравнение вформе (2.2).

Дифференциальное уравнение двигателя относительно углаповорота
будет 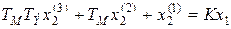, где х ₂ – угол поворота.

Величины Т_э, Т_м, K зависят от конструктивных параметров двигателя.

Дифференциальное уравнение тахогенератора может быть записано в ви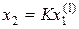де , где 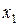– угол поворота вала тахогенератора; 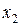– напряжение на его выходе; K – коэффициент передачи, определяемый конструктивными параметрами.