2015-05-18
463
Мультиколлениарность – это наличие линейной корреляции объясняющих переменных между собой.
Предпосылки метода наименьших квадратов проверяются как соответствующие статистические гипотезы
Независимость столбцов Xj,j=1,2..n матрицы регрессоров, число которых = к, след-но, число линейно-независимых столбцов также должно быть равно к. Число линейно-нез-х столбцов равно рангу м-цы, поэтому можно сформулировать как: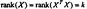 
. Если среди столбцов матрицы регрессоров есть линейно зависимые, 
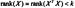и 
,т. е. матрица вырождена, значит, нет обратной матрицы. Матрица (ХTХ)-1 участвует в построении МНК-оценок, оценок их автоковар-й м-цы, оценок эндогенной переменной: Если регрессоры связаны строгой функциональной зависимостью, то это полнаямультиколлиниарность.
Полнаямулт-ть не позволяет однозначно оценить параметры исходной регрессионной модели и разделить вклады регрессоров в зависимую переменную Y.
Пусть спецификация регрессионной модели имеет вид
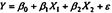и между регр-ми есть строгая линейная зависимость 
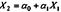. Тогда: 
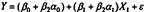Получим 
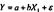, где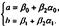 
По оценкам параметров нельзя однозначно определить параметры регрессии, =>бесчисленное множество решений.
Обычно регрессоры связаны не жесткой функц-й зависимостью, а некоторой стохастической. Это частичнаямультиколлинеарность. Если между имеется высокая степень
корреляции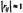 
, то матрица имеет полный ранг, но близка к
вырожденной, т. е.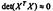 
Последствия:
• Увеличение дисперсий оценок параметров.
• Уменьшение статистик коэффициентов
• Неустойчивость МНК-оценок параметров и их дисперсий.
• Возможность получения неверного знака у
Признаки: 1) если модуль парногокоэф-та корреляции Xi,Xj
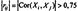1 из признаков частичноймультиколлинеарности
2) 
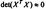3) 
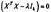,миним. собств. число матрицы приблизит-но равно нулю.
