Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Параметризация модели осуществляется следующим образом. Линейная регрессия сводится к нахождению уравнения вида:
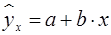 (3)
(3)
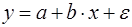 (4)
(4)
Уравнение вида 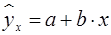 (3) позволяет по заданным значениям фактора
(3) позволяет по заданным значениям фактора 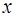 находить теоретические значения результативного признака, подставляя в него фактические значения фактора
находить теоретические значения результативного признака, подставляя в него фактические значения фактора 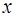 .
.
Информационный этап заключается в формировании массива исходных (фактических, эмпирических, реальных) данных хi и уi.
На этапе идентификации находят численные значения параметров 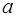 и
и 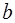 . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров
. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 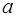 и
и 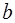 , при которых сумма квадратов отклонений фактических значений результативного признака
, при которых сумма квадратов отклонений фактических значений результативного признака 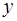 от теоретических
от теоретических 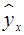 минимальна:
минимальна:
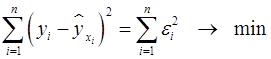 . (5)
. (5)
Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.):
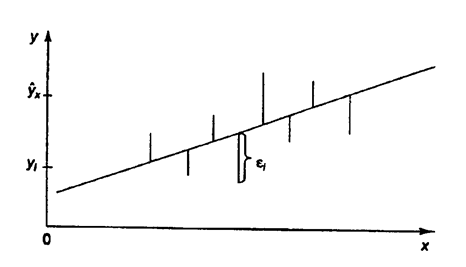
Рисунок 1.1 - Линия регрессии с минимальной дисперсией остатков.
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров 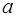 и
и 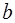 :
:
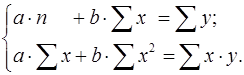 (6)
(6)
Решая систему уравнений (6), найдем искомые оценки параметров 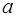 и
и 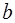 . Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (6):
. Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (6):
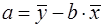 , (7)
, (7)
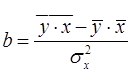 , (8)
, (8)
где 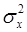 – дисперсия признака
– дисперсия признака 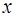 , которая рассчитывается по формулам (9.1), (10), (13) или по формулам (9.2), (10).
, которая рассчитывается по формулам (9.1), (10), (13) или по формулам (9.2), (10).
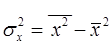 , (9.1)
, (9.1)
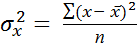 , (9.2)
, (9.2)
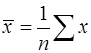 , (10)
, (10)
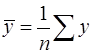 , (11)
, (11)
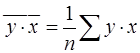 , (12)
, (12)
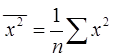 (13)
(13)
Следует отметить, что в данных формулах используются фактические значения массивов данных хi и уi.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Параметр 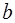 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
На этапе верификации оценивают качество полученной модели и ее пригодность для прогноза. Для этого необходимо:
- оценить тесноту связи между фактором и результатом;
- оценить качество подбора линейной функции;
- оценить значимость уравнения регрессии в целом;
- оценить значимость отдельных параметров уравнения регрессии.
Для оценки тесноты связи между фактором и результатом для линейной регрессии используют линейный коэффициент корреляции 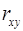 , который можно рассчитать по следующим формулам:
, который можно рассчитать по следующим формулам:
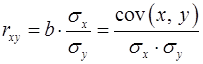 , (14)
, (14)
Между коэффициентами b и 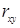 существует следующая зависимость:
существует следующая зависимость:
если b > 0, то r > 0,
если b < 0, то r < 0.
Линейный коэффициент корреляции находится в пределах: 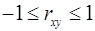 . Чем ближе абсолютное значение
. Чем ближе абсолютное значение 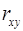 к единице, тем сильнее линейная связь между факторами (при
к единице, тем сильнее линейная связь между факторами (при 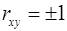 имеем строгую функциональную зависимость).
имеем строгую функциональную зависимость).
Если 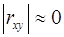 , то это может означать:
, то это может означать:
- отсутствие связи между признаками;
- наличие нелинейной формы связи.
Интерпретация значений 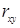 :
:
если | 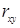 | =1 → связь тесная,
| =1 → связь тесная,
если r ≈ 0 → связи нет, или
→ связь нелинейная.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 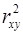 , называемый коэффициентом детерминации.
, называемый коэффициентом детерминации.
Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной 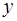 от среднего значения
от среднего значения 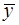 раскладывается на две части – «объясненную» и «необъясненную» (18):
раскладывается на две части – «объясненную» и «необъясненную» (18):
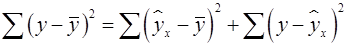 , (18)
, (18)
где 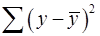 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;
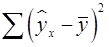 – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
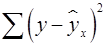 – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов (необъясненная).
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов (необъясненная).
Схема дисперсионного анализа имеет вид, представленный в таблице 1.2 (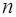 – число наблюдений,
– число наблюдений, 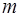 – число параметров при переменной
– число параметров при переменной 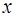 ).
).
Таблица 1.2 – Схема дисперсионного анализа
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Дисперсия на одну степень свободы |
| Общая | 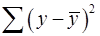 | 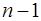 | 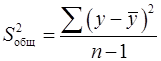 |
| Факторная | 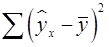 | 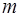 | 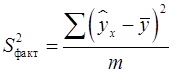 |
| Остаточная | 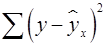 | 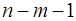 | 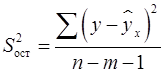 |
Коэффициент детерминации характеризует долю дисперсии результативного признака 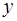 , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака:
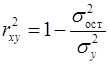 , (15)
, (15)
где 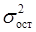 – остаточная дисперсия результативного признака (не объясненная уравнением);
– остаточная дисперсия результативного признака (не объясненная уравнением);
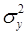 – общая дисперсия результативного признака.
– общая дисперсия результативного признака.
Остаточная дисперсия результативного признака (не объясненная уравнением) находится по формуле (16):
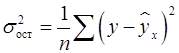 , (16)
, (16)
Общая дисперсия результативного признака находится по формуле (17.1):
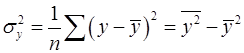 , (17)
, (17)
Соответственно величина 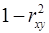 характеризует долю дисперсии
характеризует долю дисперсии 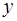 , вызванную влиянием остальных, не учтенных в модели, факторов.
, вызванную влиянием остальных, не учтенных в модели, факторов.
Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y.
Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет. При этом выдвигают основную гипотезу о незначимости уравнения в целом, которая формально сводится к гипотезе о равенстве нулю параметров регрессии, или, что то же самое, о равенстве нулю коэффициента детерминации: 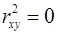 . Альтернативная ей гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии.
. Альтернативная ей гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии.
Оценка значимости уравнения регрессии в целом производится на основе 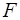 - критерия Фишера, созданного на основе теории дисперсионного анализа. Если расчетное значение Fфакт с
- критерия Фишера, созданного на основе теории дисперсионного анализа. Если расчетное значение Fфакт с 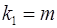 и
и 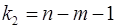 степенями свободы, где m – количество факторов, включенных в модель, больше табличного (Fтабл) при заданном уровне значимости, то модель считается значимой.
степенями свободы, где m – количество факторов, включенных в модель, больше табличного (Fтабл) при заданном уровне значимости, то модель считается значимой.
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину 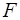 -критерия Фишера:
-критерия Фишера:
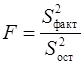 , (19)
, (19)
Фактическое значение 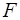 -критерия Фишера (19) сравнивается с табличным значением
-критерия Фишера (19) сравнивается с табличным значением 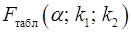 при уровне значимости
при уровне значимости 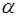 и степенях свободы
и степенях свободы 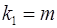 и
и 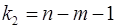 . При этом, если фактическое значение
. При этом, если фактическое значение 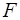 -критерия больше
-критерия больше 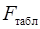 , то гипотеза о статистической незначимости уравнения в целом отклоняется.
, то гипотеза о статистической незначимости уравнения в целом отклоняется.
Для парной линейной регрессии 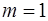 , поэтому
, поэтому 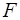 -критерий можно определить по формуле (20):
-критерий можно определить по формуле (20):
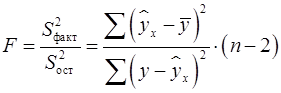 , (20)
, (20)
Величина 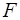 -критерия связана с коэффициентом детерминации
-критерия связана с коэффициентом детерминации 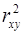 , и в линейной регрессии ее можно рассчитать по следующей формуле (21):
, и в линейной регрессии ее можно рассчитать по следующей формуле (21):
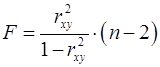 , (21)
, (21)
Значимость отдельных параметров уравнения оценивается с помощью t -статистики по формулам:
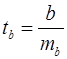 , (22)
, (22)
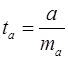 , (23)
, (23)
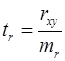 , (24)
, (24)
где 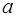 , b, rxy – параметры уравнения регрессии,
, b, rxy – параметры уравнения регрессии,
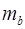 ,
, 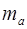 ,
, 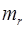 – стандартные ошибки соответствующих параметров;
– стандартные ошибки соответствующих параметров;
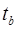 ,
, 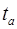 ,
, 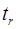 – фактические значения t-статистики или критерия Стьюдента по каждому параметру соответственно.
– фактические значения t-статистики или критерия Стьюдента по каждому параметру соответственно.
Стандартная ошибка коэффициента регрессии 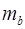 определяется по формуле (25):
определяется по формуле (25):
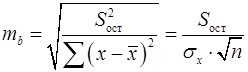 , (25)
, (25)
где 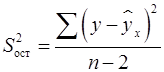 – остаточная дисперсия на одну степень свободы.
– остаточная дисперсия на одну степень свободы.
Стандартная ошибка параметра 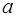 определяется по формуле (26):
определяется по формуле (26):
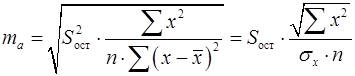 . (26)
. (26)
Стандартная ошибка параметра rxy определяется по формуле (27):
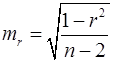 , (27)
, (27)
Для оценки существенности каждого параметра фактическое значение 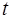 -критерия Стьюдента, определённое по формулам (22), (23), (24) сравнивается с табличным значением при определенном уровне значимости
-критерия Стьюдента, определённое по формулам (22), (23), (24) сравнивается с табличным значением при определенном уровне значимости 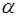 и числе степеней свободы
и числе степеней свободы 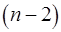 . Если
. Если 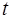 -критерий фактический больше
-критерий фактический больше 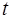 -критерия табличного, то гипотеза о статистической незначимости данного параметра отклоняется.
-критерия табличного, то гипотеза о статистической незначимости данного параметра отклоняется.
Существует связь между 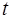 -критерием Стьюдента и
-критерием Стьюдента и 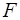 -критерием Фишера:
-критерием Фишера:
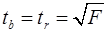 , (28)
, (28)
Таким образом, проверка гипотез о незначимости коэффициента регрессии и коэффициента корреляции проводится одинаково. Если коэффициент регрессии статистически значимый, то коэффициент корреляции тоже статистически значимый.
Для построения прогноза по уравнению регрессии необходимо подставить в уравнение 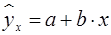 соответствующее значение
соответствующее значение 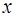 . Таким образом, определяется
. Таким образом, определяется 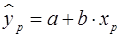 как точечный прогноз у при
как точечный прогноз у при 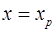 .
.
Однако точечный прогноз очень ненадежен. Вероятность того, что реальное значение у совпадет с прогнозным 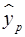 , очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определяют доверительный интервал прогноза по формуле (29):
, очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определяют доверительный интервал прогноза по формуле (29):
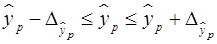 (30)
(30)
где 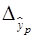 – средняя ошибка прогноза при заданной степени вероятности.
– средняя ошибка прогноза при заданной степени вероятности.
Среднюю ошибку прогноза можно определить по формуле (30):
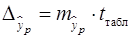 , (31)
, (31)
где 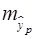 – стандартная ошибка у;
– стандартная ошибка у;
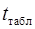 – задается самостоятельно, в соответствии со степенью свободы и желаемой вероятностью 1-α.
– задается самостоятельно, в соответствии со степенью свободы и желаемой вероятностью 1-α.
Стандартная ошибка 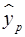 определяется по формуле (31);
определяется по формуле (31);
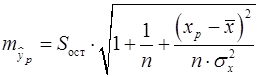 (32)
(32)
Таким образом, можно сделать вывод, что при х = хp, 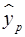 попадает в интервал
попадает в интервал 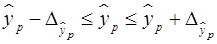 с вероятностью 1-α.
с вероятностью 1-α.
Аналогично определяется интервал допустимых значений для коэффициента корреляции b.
 2015-05-18
2015-05-18 2135
2135
