Определение. Дифференциальным уравнением второго порядка называется уравнение вида:
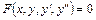 .
.
Частным решением дифференциального уравнения второго порядка называется решение, удовлетворяющее заданным начальным условиям
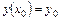 ,
, 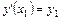 ,
,
где 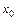 ,
, 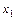 ,
, 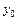 ,
, 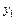 - заданные постоянные величины.
- заданные постоянные величины.
Некоторые частные случаи дифференциальных уравнений второго порядка легко приводятся к уравнениям первого порядка.
1. Левая часть уравнения не содержит 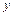 и
и 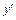 :
:
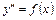 . (20)
. (20)
В этом случае пользуемся тождеством 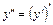 .
.
Пример 5. Решить уравнение 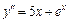 .
.
Решение.
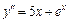 ,
,
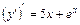 ,
,
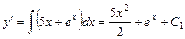 ,
,
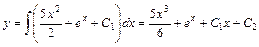 - общий интеграл.
- общий интеграл.
Ответ: 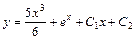 .
.
2. Левая часть уравнения не содержит 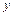 :
:
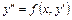 . (21)
. (21)
В этом случае пользуемся заменой 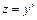 .
.
Пример 6. Решить уравнение 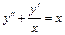 .
.
Решение. Произведем замену 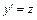 , тогда
, тогда 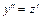 и данное уравнение обращается в уравнение первого порядка:
и данное уравнение обращается в уравнение первого порядка:
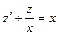 - линейное уравнение.
- линейное уравнение.
Воспользовавшись заменой 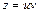 , будем иметь:
, будем иметь:
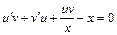 ,
,
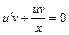 ,
,
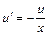 ,
,
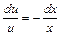 ,
,
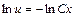 ,
,
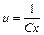 ,
,
тогда
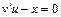 ,
,
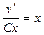 ,
,
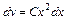 ,
,
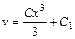 .
.
Произведем обратную замену:
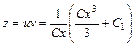 ,
,
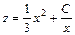 .
.
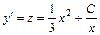 ,
,
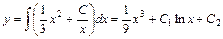 - общий интеграл.
- общий интеграл.
Ответ: 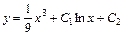 .
.
3. Левая часть уравнения не содержит  :
:
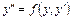 . (22)
. (22)
В этом случае полагаем 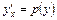 , тогда
, тогда 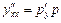 .
.
Пример 7. Решить уравнение 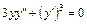 .
.
Решение. Сделаем замену 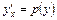 , тогда
, тогда 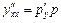 .
.
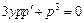 ,
,
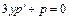 ,
,
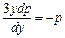 ,
,
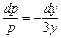 ,
,
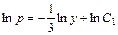 ,
,
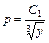 .
.
Сделаем обратную замену:
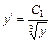 ,
,
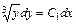 ,
,
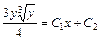 .
.
В силу произвольности констант 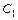 и
и 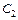
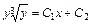
или
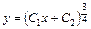 - общее решение.
- общее решение.
Ответ: 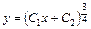 .
.
 2015-05-18
2015-05-18 324
324








