Определение. Однородным линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида
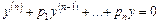 , (29)
, (29)
где 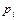 ,
, 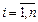 - некоторые постоянные.
- некоторые постоянные.
Если характеристическое уравнение для уравнения (29) имеет корни 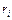 ,
, 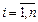 , тогда
, тогда
1) каждому 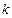 -кратному действительному корню
-кратному действительному корню 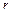 характеристического уравнения (29) соответствует
характеристического уравнения (29) соответствует 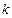 частных решений вида
частных решений вида 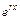 ,
, 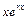 ,…,
,…, 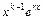 ;
;
2) каждой паре 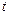 -кратных комплексно сопряженных корней
-кратных комплексно сопряженных корней 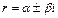 характеристического уравнения (29) соответствует
характеристического уравнения (29) соответствует 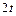 частных решений вида
частных решений вида
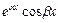 ,
, 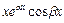 ,…,
,…, 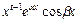 ,
,
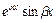 ,
, 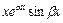 ,…,
,…, 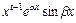 .
.
Общая сумма кратностей всех корней должна равняться степени характеристического уравнения 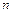 , поэтому число всех частных решений будет в точности совпадать с порядком уравнения.
, поэтому число всех частных решений будет в точности совпадать с порядком уравнения.
Чтобы найти общее решение заданного уравнения, нужно взять линейную комбинацию указанных частных решений.
Пример 9. Решить уравнение 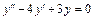 .
.
Решение. Характеристическое уравнение имеет вид:
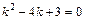 .
.
Корни этого уравнения 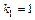 ,
, 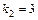 .
.
Тогда общее решение данного уравнения:
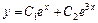 .
.
Ответ: 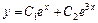 .
.
Пример 10. Решить уравнение
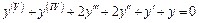 .
.
Решение. Характеристическое уравнение
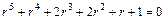 .
.
Методом подбора найдем, что один из корней 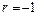 , разделим многочлен на
, разделим многочлен на 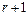 , получим:
, получим:
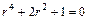 или
или 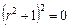 .
.
Корни этого уравнения 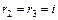 ,
, 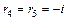 .
.
Поэтому общее решение заданного дифференциального уравнения запишется в виде:
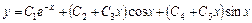 .
.
Ответ: 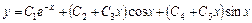 .
.
 2015-05-18
2015-05-18 341
341








