2015-05-18
404
Пусть дана бесконечная последовательность чисел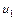 
, 
,…, 
,…
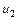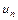Определение. Выражение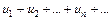 
называется числовым рядом, а 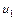, ,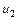…, ,… 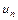- членами ряда.
Коротко ряд записывается так: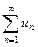 
.
Выражение для n -го члена ряда при произвольном n называется общим членом ряда.
Назовем n -ой частичной суммой ряда сумму его n первых членов:
.
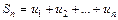Определение. Если при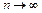 
существует конечный предел последовательности частичных сумм членов данного ряда
,
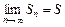то ряд называется сходящимся, а число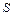 
- его суммой.
В противном случае ряд называют расходящимся.
Справедлив необходимый признак сходимости ряда: Если ряд сходится, то общий член стремится к нулю при неограниченном возрастании его номера.
Заметим, что этот признак является необходимым, но не достаточным, т.е. обратное утверждение не верно.
Пример 12. Рассмотрим ряд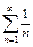 
, который называется гармоническим.
Здесь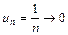 
при 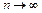, но при этом ряд расходится 
.
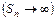Из необходимого признака сходимости ряда можно вывести достаточный признак расходимости ряда: Если общий член данного ряда при возрастании номера не стремится к нулю, то этот ряд является расходящимся.
