Уравнение вида (27), в котором правая часть не является тождественным нулем называют неоднородным дифференциальным уравнением с постоянными коэффициентами.
Справедлива теорема о структуре общего решения неоднородного уравнения (27): Общее решение уравнения с правой частью (27) можно составить как сумму общего решения соответствующего однородного уравнения и какого-либо частного решения данного уравнения.
Оказывается, что частное решение уравнения (27), где правая часть
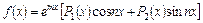 ,
,
имеет вид
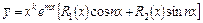 ,
,
где 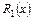 ,
, 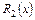 - многочлены степени, равной высшей из степеней многочленов
- многочлены степени, равной высшей из степеней многочленов 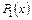 ,
, 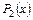 , а
, а 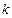 - кратность, с которой
- кратность, с которой 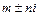 входят в число корней характеристического уравнения. Если
входят в число корней характеристического уравнения. Если 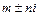 не являются корнями характеристического уравнения, то
не являются корнями характеристического уравнения, то 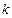 принимаем равным нулю.
принимаем равным нулю.
Пример 11. Решить уравнение 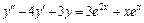 .
.
Решение. Общее решение соответствующего однородного уравнения было найдено в примере 9 и имеет вид:
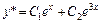 .
.
Так как величина 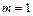 (коэффициент при
(коэффициент при  в степени второй экспоненты в правой части дифференциального уравнения) совпадает с однократным корнем
в степени второй экспоненты в правой части дифференциального уравнения) совпадает с однократным корнем 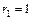 характеристического уравнения, то будем искать частное решение в виде:
характеристического уравнения, то будем искать частное решение в виде:
|
|
|
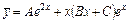 .
.
Вычислим производные функции 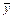 до второго порядка:
до второго порядка:
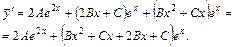
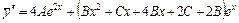 .
.
Подставим полученные производные в исходное уравнение:
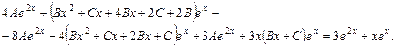
Упростим
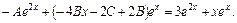
Тогда 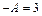 ,
,  ,
, 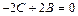 . Отсюда
. Отсюда
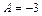 ,
, 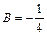 ,
, 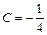 .
.
И частное решение имеет вид:
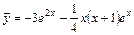 .
.
Тогда общее решение неоднородного уравнения:
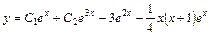 .
.
Ответ: 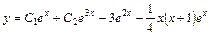 .
.
 2015-05-18
2015-05-18 366
366








