Наиболее простое уравнение, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой (однофакторное линейное уравнение регрессии):
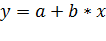 , (77)
, (77)
где a, b – параметры уравнения регрессии, которые необходимо определить;
y – результативный показатель;
x – факторный показатель.
Для нахождения параметров a, b используется метод наименьших квадратов в результате решения системы уравнений:
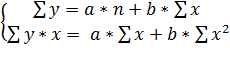 (78)
(78)
Для оценки тесноты линейной связи между 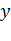 и
и 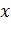 рассчитывается парный коэффициент корреляции:
рассчитывается парный коэффициент корреляции:
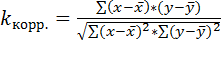 , (79)
, (79)
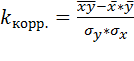 , (80)
, (80)
где  ,
, 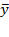 - средние значения показателей;
- средние значения показателей;
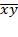 - среднее значение произведения показателей;
- среднее значение произведения показателей;
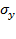 ,
, 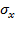 - средние квадратические отклонения значений показателей.
- средние квадратические отклонения значений показателей.
Среднее квадратическое отклонение характеризует разброс значений динамического ряда вокруг среднего арифметического уровня:
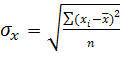 (81)
(81)
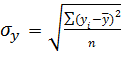 (82)
(82)
Чем выше среднее квадратическое отклонение, тем сильнее разброс вокруг среднего.
Величина 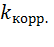 изменяется в диапазоне [-1÷1]. Если
изменяется в диапазоне [-1÷1]. Если 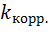 ˃0 связь между показателями прямая и увеличение
˃0 связь между показателями прямая и увеличение 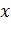 ведет к росту
ведет к росту 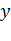 . Если
. Если 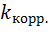 ˂0 связь между показателями обратная и увеличение
˂0 связь между показателями обратная и увеличение 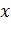 ведет к снижению
ведет к снижению 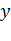 . Чем
. Чем 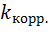 →1, тем меньше разброс колебаний между значениями и теснее между ними функциональная линейная связь. Оценка диапазонов качественной характеристики силы связи между фактором и результатом представлена в таблице 20.
→1, тем меньше разброс колебаний между значениями и теснее между ними функциональная линейная связь. Оценка диапазонов качественной характеристики силы связи между фактором и результатом представлена в таблице 20.
Таблица 20 – Качественная характеристика силы связи между показателями
Значение 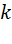
| Характеристика связи |
| Меньше 0,3 | Отсутствует |
| 0,3-0,7 | Средняя |
| 0,7-0,9 | Высокая |
| 0,9-0,99 | Весьма высокая |
| Связь не статистическая, а функциональная |
Пример. Оценить сбалансированность положительного и отрицательного денежных потоков предприятия за 3 года поквартально. В таблице 16 представлены показатели для проведения анализа.
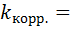
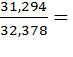 0,9
0,9
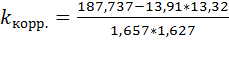 = 0,9
= 0,9
Между положительным и отрицательным денежным потоками высокая функциональная линейная связь.
Составим уравнение прямой (однофакторное линейное уравнение регрессии) по ф.77, которое поможет определить меру прироста отрицательного денежного потока (ОДП) при изменении положительного денежного потока (ПДП) на 1 тыс.р. Для нахождения a и b решим систему уравнений по ф.78.
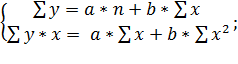
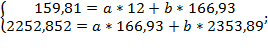
Решаем систему уравнений относительно 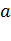 и
и 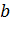 :
:
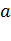 = 0,34;
= 0,34; 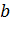 = 0,933
= 0,933
Составим однофакторное линейное уравнение регрессии:
y = 0,34 + 0,933 x
Таблица 21 – Показатели для оценки сбалансированности денежных потоков
| № квартала | Положительный денежный поток (ПДП),тыс.р.(х) | Отрицатель ный денежный поток (ОДП),тыс.р.(у) | ху |
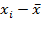
|
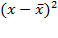
|
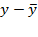
|
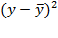
|
(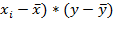
|
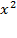
|
| 11,87 | 11,49 | 136,386 | -2,04 | 4,1616 | -1,83 | 3,349 | 3,733 | 140,89 | |
| 12,35 | 12,11 | 149,558 | -1,56 | 2,4336 | -1,21 | 1,464 | 1,887 | 152,52 | |
| 11,87 | 10,12 | 120,124 | -2,04 | 4,161 | -3,2 | 10,24 | 6,528 | 140,89 | |
| 11,4 | 11,18 | 127,452 | -2,51 | 6,3 | -2,14 | 4,58 | 5,371 | 129,96 | |
| 13,34 | 13,00 | 173,42 | -0,57 | 0,325 | -0,32 | 0,102 | 0,182 | 177,95 | |
| 14,14 | 13,56 | 191,738 | 0,23 | 0,053 | 0,24 | 0,057 | 0,055 | 199,94 | |
| 14,08 | 13,56 | 190,924 | 0,17 | 0,029 | 0,24 | 0,057 | 0,041 | 198,24 | |
| 15,21 | 15,00 | 228,15 | 1,3 | 1,69 | 1,68 | 2,822 | 2,184 | 231,34 | |
| 15,24 | 14,89 | 226,923 | 1,33 | 1,769 | 1,57 | 2,465 | 2,088 | 232,25 | |
| 15,98 | 15,12 | 241,617 | 2,07 | 4,285 | 1,8 | 3,24 | 3,726 | 255,36 | |
| 15,73 | 14,89 | 234,219 | 1,82 | 3,312 | 1,57 | 2,465 | 2,857 | 247,43 | |
| 15,72 | 14,78 | 232,341 | 1,81 | 3,276 | 1,46 | 2,131 | 2,642 | 247,12 | |
| Итого | 166,93 | 159,81 | 2252,852 | 31,7952 | 32,972 | 31,294 | 2353,89 | ||
Средняя 
| 166,93/12 = 13,91 | ||||||||
Средняя 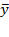
| 159,81/12 = 13,32 | ||||||||
Средняя 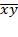
| 187,737 | ||||||||
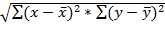 = = 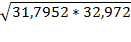 = 32,378 = 32,378
| |||||||||
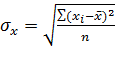 = = 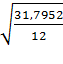 = 1,627 = 1,627
| |||||||||
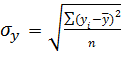 = = 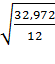 = 1,657 = 1,657
|
Уравнение регрессии показывает, что прирост ПДП на 1 тыс.р. вызывает прирост ОДП на 0,933 тыс.р.
Во многих практических случаях модель линейной регрессии, которая описывает взаимосвязи переменных y и x, является слишком упрощенной. Значение y может быть определено рядом переменных: x1, x2, x3…. В таких случаях используется модель построения уравнения множественной регрессии.
 2015-05-18
2015-05-18 896
896








