Задание 8. Найдите площадь фигуры, ограниченной указанными линиями

Найдите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.

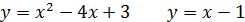
Решение:

Сделаем чертеж:

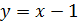– прямая,

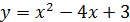– парабола, ветви направлены вверх, ось симметрии х = .

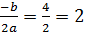Найдем точки пересечения параболы 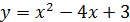и прямой 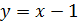, решив систему этих уравнений:

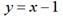
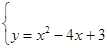
Получим:

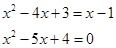
Решая данное уравнение, получим:

D = 5² – 4·1·4 = 25 - 16= 9 = 3²;

х₁ = ;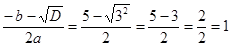

х₂ = .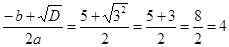

ГРАФИК ПРИЛОЖЕН ОТДЕЛЬНЫМ ФАЙЛОМ

Проецируя фигуру на ось абсцисс, видим, что искомая площадь – это площадь фигуры, заключенной между кривыми; при этом на отрезке [1;4]:

.

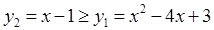Применим формулу для вычисления площадей плоских фигур

,

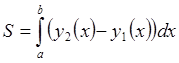где пределами интегрирования будут абсциссы точек О и А:

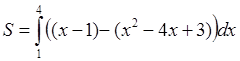
С помощью формулы Ньютона-Лейбница вычислим значение площади фигуры:

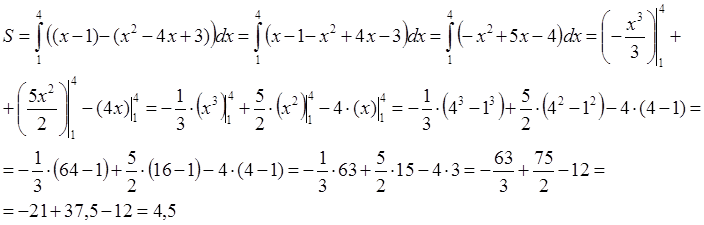
Ответ: S = 4,5 (ед ²).