Решение. Канонические уравнения

Канонические уравнения:

– эллипса ;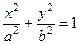

– гиперболы 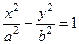или .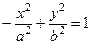

1. Преобразуем уравнение 4 x ² + 36 y ² – 576 = 0 к каноническому виду

4 x ² + 36 y ² = 576 Þ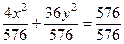

или

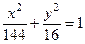– уравнение эллипса.

Таким образом, 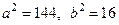. Тогда .

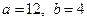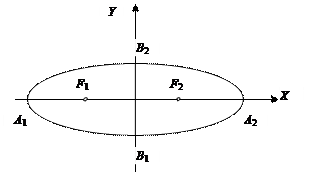
Вершины эллипса (точки пересечения эллипса с координатными осями) имеют координаты: .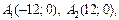

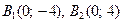Так как 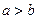, то фокусы расположены на большей оси, т.е. на оси Ох. Тогда координаты фокусов - 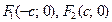, и эксцентриситет кривой - 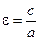, где 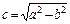= 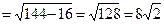, т.е. .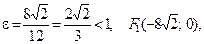

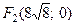2. Преобразуем уравнение 5 x ² – 16 y ² + 80 = 0 к каноническому виду

5 x ² – 16 y ² = 80 Þ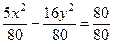

или

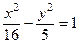- уравнение гиперболы.

Таким образом, 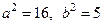. Тогда .

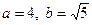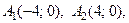
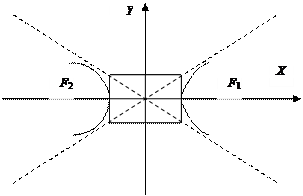
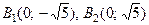- точки пересечения характеристического прямоугольника с осями Ox и Oy.

Так как ось Ох является действительной, то фокусы расположены на оси Ох. Тогда координаты фокусов - 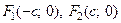, и эксцентриситет кривой - 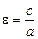, где 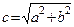= 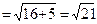, т.е. .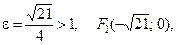

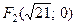Уравнения асимптот гиперболы имеют вид: 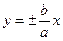, т.е.

.

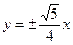Задание № 5. Даны уравнения парабол.

1. Указать ось симметрии.

2. Найти координаты фокуса и написать уравнение директрисы для каждой из парабол.

3. Построить графики заданных парабол:

а) у ² – 25 х = 0; б) х ² + 10 у = 0.