Решение. 1. Каноническое уравнение эллипса имеет вид

1. Каноническое уравнение эллипса имеет вид:

.

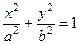Так как эллипс проходит через точки 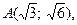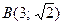, то координаты этих точек удовлетворяют уравнению эллипса. Подставив в уравнение эллипса координаты данных точек, получим систему уравнений

Таким образом, искомое уравнение имеет вид:

.

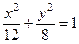2. По условию имеем:

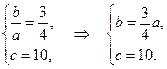
Для гиперболы 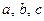связаны соотношением 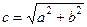или 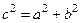. Поэтому получим уравнение 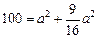или 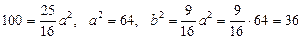. Таким образом, искомое уравнение имеет вид:

.

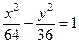3. Каноническое уравнение параболы в данном случае 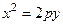, а уравнение её директрисы 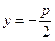. По условию задачи уравнение директрисы 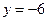. Поэтому 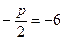или р = 12. Искомое каноническое уравнение параболы имеет вид:

.

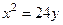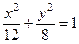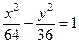ОТВЕТ: а) ; б) ; в) ..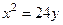

ЗАДАНИЕ № 7. Написать уравнение плоскости, проходящей через точку M (2;-4;5) перпендикулярно вектору 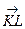, где K (1;-6;7), L (8;3;1).