2015-05-18
2531
1. Воспользуемся формулой уравнения прямой, проходящей через две данные точки:
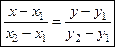. (2)
подставляя координаты точек А и В, получим уравнение прямой (АВ)
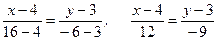
или
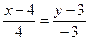
или
.
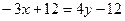Из последнего равенства получим:
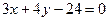- уравнение стороны (АВ).
Аналогично получим уравнение прямой (АС)
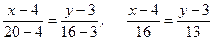
или
.
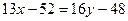Из последнего равенства получим:
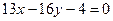- уравнение стороны (АС).
Длину стороны (АВ) вычислим по формуле (1)
.
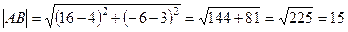2. Уравнение стороны (АВ): 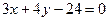запишем в виде уравнения с угловым коэффициентом (
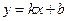), т.е. 
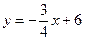. Тогда 
.
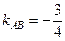Так как высота (СД) перпендикулярна (АВ), то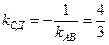 
.
Для составления уравнения прямой (СД) воспользуемся уравнением прямой, проходящей через данную точку с известным угловым коэффициентом:
|
(3)
Подставляя в это уравнение координаты точки С (20; 16) вместо (х 0; y 0) и учитывая, что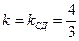 
, получим
у – 16 =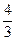 
(х – 20)
или
.
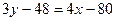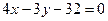- уравнение высоты (СД).
Длину высоты (СД) можно найти по формуле расстояния от точки (х 0; y 0) до прямой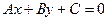 
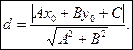(4)
Подставляя координаты точки С (20; 16) найдём расстояние от этой точки до прямой (АВ), т.е. длину высоты:
.
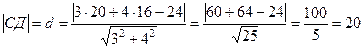3. Найдём координаты точки М. Так как М – середина отрезка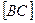 
, то
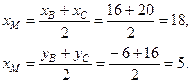
Уравнение медианы (АМ) составим по формуле (2):
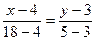
или
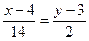Þ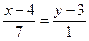 
или
.
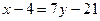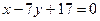- уравнение прямой (АМ).
4. Точку N пересечения медианы (АМ) и высоты (СД) найдём, решив совместно систему их уравнений
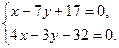
Первое уравнение системы умножим на (-4) и прибавим ко второму
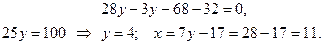
Таким образом, N (11; 4).
5. Составим уравнение прямой (L), проходящей через вершину С (20; 16) параллельно стороне (АВ).
Так как (L) ÷÷ (АВ), то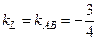 
и уравнение прямой (L) можно составить по формуле (3)
y – 16 =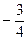 
(x – 20)
или
4 y – 64 = -3 x + 60
или
3 x + 4 y – 124 = 0 – уравнение прямой (L).
6. В пункте 1) найдено уравнение прямой (АС):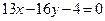 
. Найдём расстояние от точки В (16; -6) до стороны (АС)
.
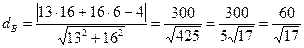7. Угол при вершине А найдём по формуле угла между двумя прямыми:
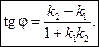(5)
Пусть в нашем случае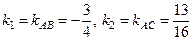 
, тогда
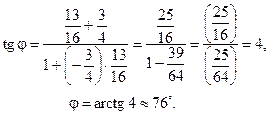
З а м е ч а н и е. Угол между двумя прямыми заданными общими уравнениями можно найти по формуле:
.
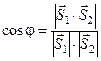(АВ): 3 x + 4 y – 24 = 0 Þ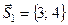 
,
(АС): 13 x - 16 y – 4 = 0 Þ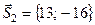 
,
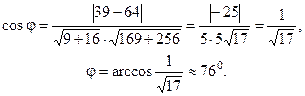
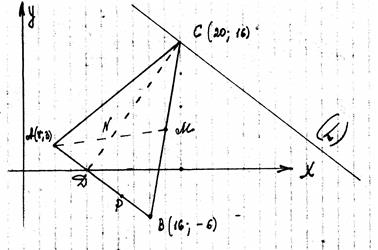
8. Прямая (АВ) перпендикулярна (СД). Поэтому искомая точка Р расположена симметрично точке А относительно (СД) и лежит на прямой (АВ). Кроме того точка Д является серединой отрезка [ АР ].
Найдём координаты точки Д, решив совместно систему уравнений прямой (АВ) и высоты (СД)
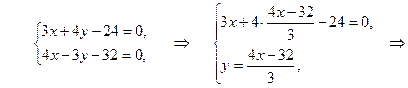
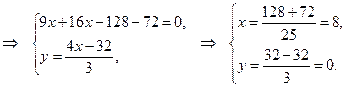
Таким образом, Д (8; 0).
Применяя формулы деления отрезка на равные части, найдём координаты точки Р
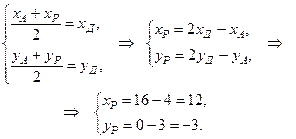
Таким образом, точка симметричная точке А относительно прямой (СД) есть точка Р (12; -3).
Задание № 3. Найти координаты центра и радиус окружности x 2 + y 2 – 6 x + 4 y – 3 = 0. Выполнить чертёж.
