Канонические уравнения параболы имеют вид 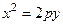 или
или 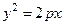 . Вершина параболы
. Вершина параболы 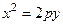 находится в точке
находится в точке 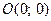 , ось симметрии - ось Оy; для параболы
, ось симметрии - ось Оy; для параболы 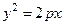 осью симметрии является ось Ох, вершина также расположена в точке
осью симметрии является ось Ох, вершина также расположена в точке 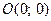 . Фокусы расположены на оси симметрии:
. Фокусы расположены на оси симметрии: 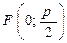 и
и 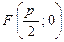 соответственно для
соответственно для 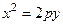 и
и 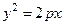 . Директриса – прямая, перпендикулярная оси симметрии и не пересекающая параболу. Уравнение директрисы:
. Директриса – прямая, перпендикулярная оси симметрии и не пересекающая параболу. Уравнение директрисы: 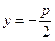 и
и 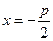 соответственно для
соответственно для 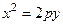 и
и 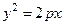 .
.
1. Преобразуем уравнение у 2 – 25 х = 0 к каноническому виду:
у 2 = 25 х
или
у 2 = 2 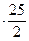 х.
х.
Осью симметрии этой параболы является ось Ох, поэтому фокус расположен на этой оси: 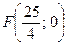 , уравнение директрисы имеет вид
, уравнение директрисы имеет вид 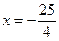 .
.
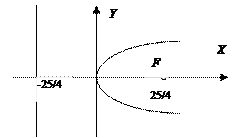
2. Преобразуем уравнение х 2 + 10 у = 0 к каноническому виду:
х 2 = -10 у
или
х 2 = 2×(-5) у.
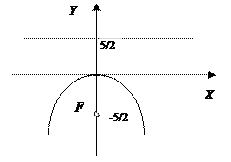
Осью симметрии этой параболы является ось Оy, поэтому фокус расположен на этой оси: 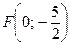 , уравнение директрисы имеет вид:
, уравнение директрисы имеет вид:
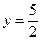 .
.
Задание № 6. Составить канонические уравнения:
а) эллипса, проходящего через точки 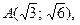
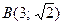 ;
;
б) гиперболы, асимптотами которой служат прямые 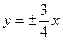 , а один из фокусов находится в точке (-10; 0);
, а один из фокусов находится в точке (-10; 0);
в) параболы, имеющей директрису 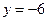 .
.
 2015-05-18
2015-05-18 589
589








