2015-05-20
468
1-10. Решить следующие задачи:.
1. По уравнению сторон треугольника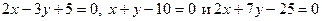 
найти координаты его вершин. Сделать построение.
2. Написать уравнение прямой, проходящей через точку пересечения прямых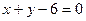 
, 
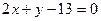и отсекающей на осях координат равные положительные отрезки. Сделать построение.
3. При каком значении С прямая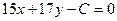 
будет проходить через точку пересечения прямых 
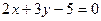и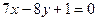 
? Построить.
4. Даны уравнения сторон треугольника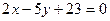 
, 
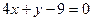и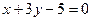 
. Составить уравнение прямой, проходящей через вершину треугольника параллельно его стороне, образующей с осью абсцисс острый угол. Построить.
5. Треугольник задан уравнениями: (АВ)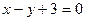 
, (АС) 
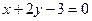и
(ВС)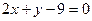 
. Составить уравнение высоты, опущенной из вершины В. Построить.
6. Даны уравнения двух смежных сторон параллелограмма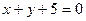 
, 
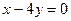. Найти уравнение двух других сторон, если известна точка пересечения его диагоналей (2;2). Построить.
7. Уравнения смежных сторон прямоугольника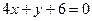 
и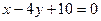 
. Координаты одной из вершин С(3;-3). Составить уравнение диагонали, проходящей через точку С. Построить.
8. По уравнениям сторон треугольника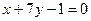 
, 
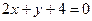и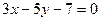 
. Составить уравнение высоты, опущенной из вершины, лежащей в третьей четверти. Построить.
9. Составить уравнение перпендикуляра к прямой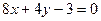 
в точке пересечения ее с прямой 
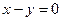. Построить.
10. По уравнениям прямых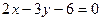 
; 
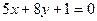найти расстояние между точками их пересечения с осью ординат. Построить.
11-20. Дано общее уравнение кривой второго порядка F(x,y)=0.
1) Преобразовать уравнение к каноническому виду;
