Предел функции

Рассмотрим функцию у =f(x), определенную в некотором ин­тервале, содержащем точку х= а.

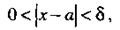Число А называется пределом функции у =f(x) при х, стремя­щемся к а (или в точке а), если для любого числа 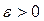существует та­кое 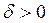, что при всех х, удовлетворяющих условию

(4)

выполняется неравенство

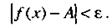(5)

Обозначения предела функции f(x)при x, стремящемся к а:

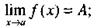(6)

Рассмотрим также односторонние пределы функции: предел слева 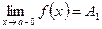, (х стремится к а, оставаясь меньше а: х < а) и предел справа 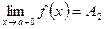(х стремится к а, оставаясь больше а: х>а)

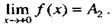
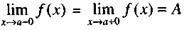Когда а = 0, то вместо 0-0 пишут -0, вместо 0 +0 пишут +0, поэтому последние формулы принимают вид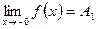

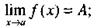Если односторонние пределы равны то предел А в точке х = а существует и равен односторонним пределам

Из определения предела функции следует, что предел постоянной равен этой постоянной.

Если односторонние пределы различны 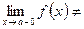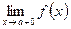, или хотя бы один из них не существует, то не существует и предел функции в точке х = а.

Функция 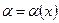называется бесконечно малой при х 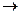а (или при х 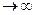), если

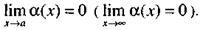
Свойства бесконечно малых выражаются следующими теоре­мами.