Теорема 5.2. Если функция непрерывна в точке х0 , а функция непре­рывна в точке , то сложная функция

Если функция 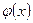непрерывна в точке х₀, а функция 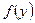непре­рывна в точке 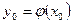, то сложная функция 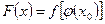непре­рывна в точке х₀.

Рассмотрим функцию у =f(x), определенную на интервале (а, b), кроме, быть может, точки 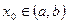. Точка х₀ называется точкой разрыва данной функции, если в ней функция определена, но не явля­ется непрерывной, или не определена в этой точке.

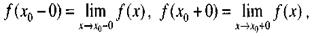Если х₀ - точка разрыва функции f(x) и существуют конечные пределы

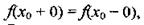то она называется точкой разрыва первого рода.

Пусть функция у =f(x) имеет разрыв в точке х₀ и

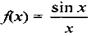тогда х₀ называется точкой устранимого разрыва

Например, для функции является точкой устранимого разрыва.

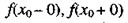Если х₀ - точка разрыва и по крайней мере один из пределов является бесконечным или не существует, то х₀ называется точкой разрыва второго рода.

Функция называется непрерывной на интервале, если она не­прерывна в каждой точке этого интервала.

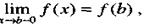
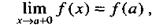Если функция определена при х = а и при этом то говорят, что f(x) в точке а непрерывна справа.

Аналогично, если

то говорят, что в точке b эта функция непрерывна слева.

Функция называется непрерывной на отрезке [а, b], если она непрерывна в каждой его точке (в точке а - непрерывна справа, в точ­ке b - непрерывна слева).

Наибольшим значением функции у = f(x) на отрезке [а, b] назы­вается такое ее значение f(x₁), что f(x) 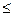f(x₁) при всех x 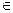[а, b].

Наименьшим значением функции у = f(x) на отрезке [а, b] назы­вается такое ее значение f(x₂), что f(x₂) 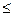f(x) для всех. x 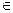[а, b].

Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.