Экспоненциальное распределение

Экспоненциальное распределение характерно для внезапных отказов элементов и систем. Плотность вероятности экспоненциального распределения задается уравнением

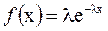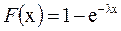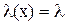, , ,x > 0,(1.43)

где l - параметр распределения, являющийся строго положительной константой.

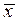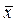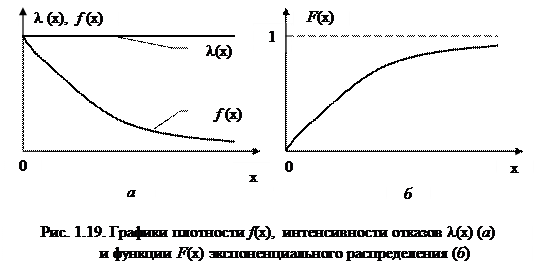
Среднее значение и среднеквадратическое отклонение σ экспоненциального распределения совпадают и равны обратному значению параметра = = 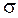1/l. Графики функций F (х) и f (x) приведены на рис. 1.19. Отличительной особенностью экспоненциального распределения является то, что интенсивность отказов l(х) постоянна, т.e.не зависит от аргумента (значения случайной величины).

Основное свойство экспоненциального закона состоит в том, что при нем вероятность безотказной работы на данном интервале не зависит от времени предшествующей работы, а зависит от длины интервала. Это значит, что будущее поведение элемента не зависит от прошлого, если в данный момент он исправлен.

Применимость экспоненциального закона зависит в основном от характера отказов. Как уже сказано, внезапные отказы случайного характера хорошо описываются экспоненциальным законом, но отказы, связанные с износом, не следуют этому закону. Если учитывается сезонная нестационарность потока отказов, то поток отказов не будет простейшим и экспоненциальный закон не применим. Аналогичное запрещение накладывается в случае учета начальных отказов.