Усеченное нормальное распределение

Усеченное нормальное распределение случайной величины – это такое распределение, для которого в крайних областях (х < а, х > b) плотность распределения принимается равной нулю; при этом усеченное распределение принимает вид:

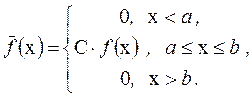(1.37)

Из условия нормировки

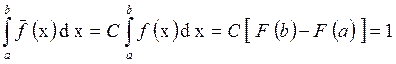
следует формула для коэффициента

C = 1/ [ F (b) – F (a)], (1.38)

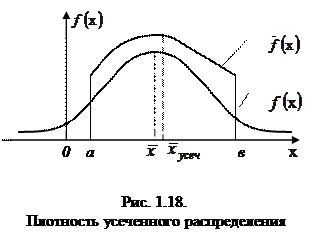
где F - функция основного (не усеченного) распределения. Указанные распределения представлены на рис. 1.18.

Приведем основные формулы для усеченного распределения:

,

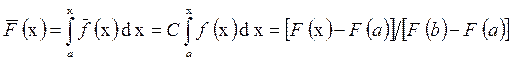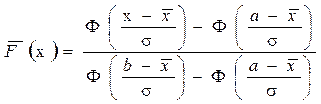, (1.39)

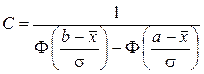. (1.40)

В этих формулах 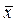и s относятся к основному распределению.

В частном случае для описания распре­деления положительных случайных величин (при х < 0, f (х) = 0) формулы усеченного нормального распределения при а = 0 и 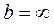имеют следующий вид:

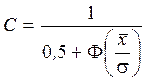; (1.41)

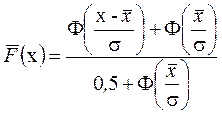. (1.42)