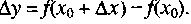Понятие производной, ее геометрический и физический смысл

Рассмотрим функцию у =f(х)., заданную в интервале (а, b); пусть 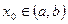,и 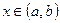тогда приращение функции в точке х₀ выразится формулой

Производной функции у =f(х) в точке x 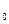называется предел от­ношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю.

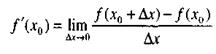Производную функции у =f(х) в точке x 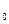обозначают символом 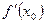(читается: эф штрих от x 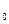). Следовательно, по опреде­лению

(2)

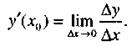или

(3)

Из формул (1) и (2) следует, что

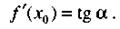(4)

Формула (4) выражает геометрический смысл производной: производная от данной функции в данной точке равна тангенсу угла между осью Ох и касательной к графику этой функции в соответст­вующей точке.

Уравнение касательной к линии у =f(х) в точке М₀(х₀, у₀) при­нимает вид

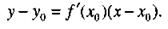(5)

Нормалью к кривой в некоторой ее точке называется перпенди­куляр к касательной в той же точке. Если 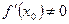, то уравнение нор­мали к линии у =f(х) в точке М₀(х₀, у₀) записывается так:

(6)

Физический смысл производной состоит в следующем: производная от пути по времени равна скорости прямолинейного движения точки.

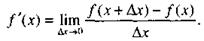Если в формуле (2) от точки х₀ перейти к другой точке х, по­лучим другой предел, поэтому 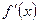- некоторая функция аргумента х:

(7)