Задача о касательной

Касательной к линии l в точке М₀ называется прямая М₀T- предельное положение секущей М₀ M, когда точка М стре­мится к М₀ вдоль данной линии (т.е. угол 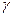стремится к нулю) про­извольным образом.

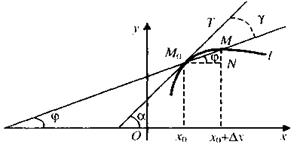Задача о касательной состоит в следующем: написать уравнение касательной к линии у =f(х) в точке М₍₎(х 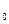, у₀).

Введем декартову прямоугольную систему координат Оху, рас­смотрим график функции у =f(х). Пусть М₀(х₀, у₀) - фиксированная точка этого графика и М(х, у) - любая другая его точка, где

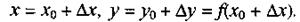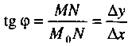Из треугольника М 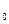МN находим, где 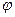- угол, образуемый секущей М₀ M с осью Ох.

Пусть М 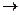М₀ вдоль графика у =f(х), М₀Т - касательная к не­му в точке Мо, 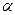- угол наклона касательной к оси Ох, тогда 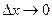, 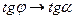. Следовательно,

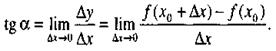(1)

Таким образом, задача о касательной приводит к необходимости рассмотрения предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.