Найти значение биомассы в момент T=12, если в начальный момент (при t=0) значение биомассы m  =10 и k(t)=
=10 и k(t)= 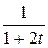 .
.
Составим дифференциальное уравнение, описывающее динамику развития популяции. Скорость изменения биомассы характеризуется производной m 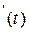 (при этом m
(при этом m  >0- это скорость развития, при этом m
>0- это скорость развития, при этом m  <0- скорость вымирания).
<0- скорость вымирания).
По условию задачи 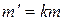 или
или 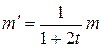 .
.
Уравнение (1) является дифференциальным уравнением с разделяющимися переменными. Разделим переменные m и t:
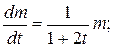
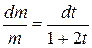
Отсюда после интегрирования левой и правой частей уравнения получаем
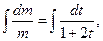 т. е.
т. е.
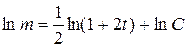
(в данном случае произвольную постоянную удобно взять в виде ln C).Из последнего равенства следует формула для общего решения дифференциального уравнения
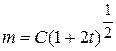 (2)
(2)
Для определения значения произвольной постоянной. С полагаем в равенстве (2) t=0, m= 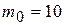 .В результате получаем
.В результате получаем
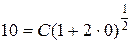 ;С=10.
;С=10.
Таким образом, из общего решения дифференциального уравнения приходим к выражению
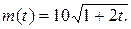 (3)
(3)
Положим теперь в равенстве (3) t=T=12. Тогда
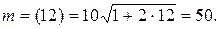
Следовательно, в момент T=12 (ед.) значение биомассы будет составлять 50(ед.).
9. Решить задачи 41-50, используя основные теоремы теории вероятностей
1. В стаде 40% овец черного цвета. Найти вероятность того, что из двух наугад выбранных овец:
а) обе окажутся черного цвета;
б) хотя бы одна окажется черного цвета.
2. В стаде 60% овец черного цвета. Найти вероятность того, что из трех наугад выбранных овец:
а) только одна окажется черного цвета;
б) только две окажутся черного цвета.
3. На складе 70% досок хвойных пород. Найти вероятность того, что из трех наугад взятых досок:
а) все три окажутся из хвойных пород;
б) ни одной не будет хвойной породы.
4. Всхожесть зерна 90%. Найти вероятность того, что из трех наугад посеянных зерен взойдут:
а) только одно;
б) только два;
в) все три зерна.
5. Известно, что при посадке погибает 1/4 саженцев. Найти вероятность того, что из четырех посаженных саженцев приживутся:
а) все три;
б) только один;
в) хотя бы один саженец.
6. В некотором водоеме лещи составляют 70% от всего количества рыбы. Какова вероятность того, что из трех выловленных рыб окажется:
а) только один лещ;
б) все три леща.
7. Вывод поголовья цыплят в инкубаторе составляет в среднем 80%. Какова вероятность того, что из трех заложенных в инкубатор яиц выведется:
а) три цыпленка;
б) хотя бы один цыпленок.
8. Всхожесть семян гороха 60%. Найти вероятность того, что из наугад взятых четырех семян гороха взойдет:
а) хотя бы одно;
б) только одно.
9. В партии хлопка содержится 70% коротких волокон. Найти вероятность того, что из трех наугад взятых волокон:
а) все три окажутся короткими;
б) хотя бы одно окажется коротким;
в) ни одно не будет коротким.
10. Известно, что при посадке погибает 1/3 саженцев. Найти вероятность того, что из трех посаженных саженцев приживутся:
а) все три;
б) только один;
в) хотя бы один саженец.
11. Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырех посеянных семян взойдут три.
12. Принимая вероятность рождения телочки и бычка одинаковыми, найти вероятность того, что среди 6 родившихся телят 4 бычка.
13. В хлопке число длинных волокон 80%. Какова вероятность того, что среди взятых наудачу 5 волокон окажется 3 длинных?
14. Доля витаминизированного комбикорма, поступившего на ферму составляет 10%. Какова вероятность того, что среди 4 мешков комбикорма, поступивших на ферму будет 2 мешка с витаминизированным комбикормом?
15. В некотором хозяйстве коров бестужевской породы составляют 70% от всего количества коров. Какова вероятность того, что из трех наугад взятых коров окажется:
а) хотя бы одна бестужевской породы;
б) все три бестужевской породы.
16. Вероятность того, что комбайн проработает в течении недели без поломок, равна 0,3. Какова вероятность того, что в звене из 4 комбайнов за неделю ремонта потребует 1 комбайн?
17. Вероятность того, что корова даст в день более15 литров молока 0,7. Найти вероятность того, что из отобранных наугад 4 коров 2 дадут более 15 литров.
18. Среди хранящихся на складе доильных аппаратов 20% неисправных. Какова вероятность того, что из 6 взятых 3 аппарата окажутся исправными?
19. Всхожесть семян фасоли 60%. Найти вероятность того, что из наугад взятых четырех семян взойдет:
а) хотя бы одно;
б)все взойдут.
20. Всхожесть зерна 95%. Найти вероятность того, что из трех наугад посеянных зерен взойдут:
а) хотя бы одно;
б) только два;
в) все три зерна.
Решение типовой задачи
Решить задачу, используя основные теоремы теории вероятностей.
В стаде 65% коров бестужевской породы. Найти вероятность того, что из трех наугад выбранных коров окажется: а) все три бестужевской породы; б) только одна бестужевской породы; в) только две бестужевской породы; г) ни одной бестужевской породы; д) хотя бы одна бестужевской породы.
Решение. Если в стаде 65% коров бестужевской породы, то это означает, что вероятность того, что случайно отобранная корова будет этой породы, равна р=0.65.
Вероятность противоположного события, т.е. того, что корова будет другой породы, равна q=1 - p=1 - 0.65=0.35.
а) Вероятность того, что все три случайным образом отобранные коровы окажутся бестужевской породы, находится по теореме умножения независимых событий и будет равна:
P(A)=p*p*p=0.65*0.65*0.65=0.2746.
б) Вероятность того, что только одна из трех случайным образом отобранные коровы окажутся бестужевской породы, означает, что при этом две другие не бестужевской породы. Поэтому используем теорему умножения независимых событий. Так как таких ситуаций три, то получим:
Р(А)=p*q*q + q*p*q + q*q*p=3 p*q*q=3*0.65*0.35*0.35=0.2389.
в) Вероятность того, что только две из трех случайным образом отобранные коровы окажутся бестужевской породы по аналогии с предыдущим случаем, находится по формуле:
P(A)=p*p*q + p*q* p+ q*p*p=3 p*p*q=3*0.650.35=0.4436.
г) Вероятность того, что ни одна из трех случайным образом отобранные коровы окажутся бестужевской породы, найдем по теореме умножения независимых событий:
P(A)=q*q*q=0.35*0.35*0.35=0.0429.
д) Вероятность того, что хотя бы одна из трех случайным образом отобранных коров окажется бестужевской породы, находится как разность между единицей и произведением вероятностей противоположного события.
P(A)=1 - q*q*q=1 - 0.35*0.35*0.35=1 - 0.0429=0.9571.
1. Шипачев В.С, Высшая математика: Учеб./под ред. А.Н. Тихонова. – 2-е изд. стереотип. – М.: Высш. шк., 1990. – 479 с.
2. Письменный Д.Т. Конспект лекций по высшей математике. I, IIч.. –М.:Рольф, 2002. – 288с.
3. Зайцев И.А. Высшая математика: Учеб. – М.: Высш. шк., 1991. – 400с.
4. Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2ч. – М.: Высш. шк. Т.1. – 1999. – 304 с.
5. Шипачев В.С. Задачник по высшей математике: Учеб. пособие. – 2-е изд.,
испр. – М.: Высш. шк., 2000. – 304 с.
Лицензия РБ на издательскую деятельность №0261 от 10 апреля 1998 года
Подписано в печать __________2006г. Формат. Бумага типографская. Гарнитура Таймс. Усл. печ. л.___. Усл. изд. л._____. Тираж____экз. Заказ №__.
Издательство Башкирского Государственного Аграрного Университета.
Типография Башкирского Государственного Аграрного Университета.
Адрес издательства и типографии: 450001, г. Уфа, ул. 50 лет Октября, 34.
 2015-05-20
2015-05-20 3050
3050








