а) Найти интеграл
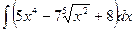
Решение:
Воспользуемся следующими свойствами неопределенного интеграла:
1. постоянной множитель можно выносить за знак интеграла, то есть
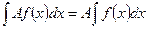
2. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) интегралов от каждой функции в отдельности, то есть
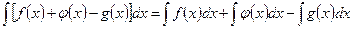
Преобразуем подынтегральную функцию в интеграле а) и воспользуемся формулой 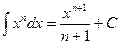 из таблицы основных неопределенных интегралов:
из таблицы основных неопределенных интегралов:
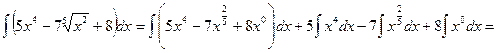
= 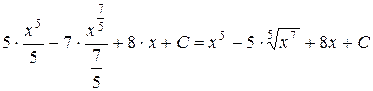
б) Найти интеграл
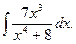
Решение:
Воспользуемся подстановкой 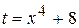 . Тогда
. Тогда 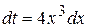 ,откуда
,откуда 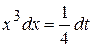 .Таким образом,
.Таким образом,
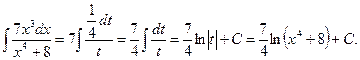
в) Найти интеграл
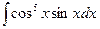
Решение:
Воспользуемся подстановкой 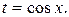
Тогда 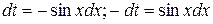 . Таким образом,
. Таким образом,
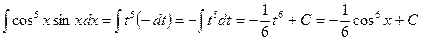
7. В задачах 1-20 вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую площадь.










Решение типовой задачи
Задача. Вычислить площадь фигуры, ограниченной параболой
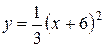 и прямой
и прямой 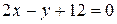 .
.
Решение:
Площадь фигуры, ограниченной сверху непрерывной кривой у=f(х), снизу непрерывной кривой 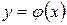 , слева прямой х=а, справа прямой х=b, вычисляется по формуле:
, слева прямой х=а, справа прямой х=b, вычисляется по формуле:
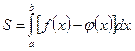 (1)
(1)
Если кривые у=f(х) и 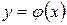 образуют замкнутую линию, то точки а и b совпадают с абсциссами точек пересечения этих кривых. Найдем точки пересечения заданных параболы и прямой. Для этого решим систему их уравнений:
образуют замкнутую линию, то точки а и b совпадают с абсциссами точек пересечения этих кривых. Найдем точки пересечения заданных параболы и прямой. Для этого решим систему их уравнений:
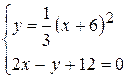
Приравняв значения у из обоих уравнений, получим:
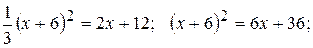
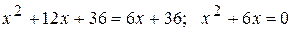
Отсюда 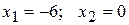 .Таким образом, парабола пересекается с прямой в точках А(-6;0) и В(0;12).
.Таким образом, парабола пересекается с прямой в точках А(-6;0) и В(0;12).
Искомая фигура изображена на рисунке.
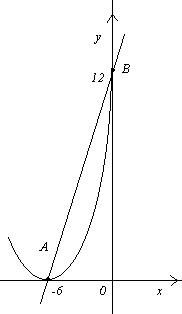
Из формулы (1) следует, что площадь фигуры равна
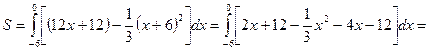
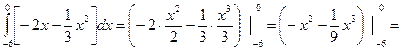
= 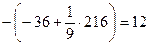
Следовательно, искомая площадь равна 12 кв. ед.
8. Требуется составить дифференциальное уравнение динамики развития некоторого биологического вида и найти решение этого уравнения. Состояние популяции (в простейшем понимании - стада) можно охарактеризовать массой m этой популяции (то есть весом всего стада), причем масса m является функцией времени m=m(t), Считая, что скорoсть прироста биомассы пропорциональна биомассе популяции с коэффициентом k=k(t) и что известна начальная биомасса m  (при t=0), найти величину биомассы в момент t=T.
(при t=0), найти величину биомассы в момент t=T.
1. m  = 12; T=2; k(t)=
= 12; T=2; k(t)= 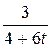 .
.
2. m  =18; T=18; k(t)=
=18; T=18; k(t)= 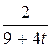 .
.
3. m  =9; T=8; k(t)=
=9; T=8; k(t)= 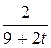 .
.
4. m  =12; T=2; k(t)=
=12; T=2; k(t)= 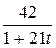 .
.
5. m  =14; T=3; k(t)=
=14; T=3; k(t)= 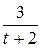 .
.
6. m  =10; T=2; k(t)=
=10; T=2; k(t)= 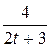 .
.
7. m  =1; T=12; k(t)=
=1; T=12; k(t)= 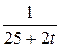 .
.
8. m  =5; T=4; k(t)=
=5; T=4; k(t)= 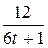 .
.
9. m  =18; T=2; k(t)=
=18; T=2; k(t)= 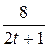 .
.
10. m  =8; T=2; k(t)=
=8; T=2; k(t)= 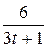 .
.
11. m  = 2; T=2; k(t)=
= 2; T=2; k(t)= 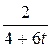 .
.
12. m  =8; T=18; k(t)=
=8; T=18; k(t)= 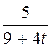 .
.
13. m  =19; T=8; k(t)=
=19; T=8; k(t)= 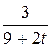 .
.
14. m  =22; T=2; k(t)=
=22; T=2; k(t)= 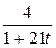 .
.
15. m  =24; T=3; k(t)=
=24; T=3; k(t)= 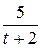 .
.
16. m  =4; T=2; k(t)=
=4; T=2; k(t)= 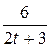 .
.
17. m  =7; T=12; k(t)=
=7; T=12; k(t)= 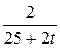 .
.
18. m  =15; T=4; k(t)=
=15; T=4; k(t)= 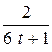 .
.
19. m  =8; T=2; k(t)=
=8; T=2; k(t)= 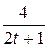 .
.
20. m  =18; T=2; k(t)=
=18; T=2; k(t)= 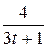 .
.
 2015-05-20
2015-05-20 1474
1474
