Собранный в процессе статистического наблюдения материал представляет собой разрозненные первичные сведения об отдельных единицах изучаемого явления. В таком виде материал еще не характеризует явление в целом: не дает представление ни о величине (численности) явления, ни о его составе, ни о размере характерных признаков, ни о существе связей этого явления с другими явлениями и т.д. Указанные сведения нельзя получить непосредственно из наблюдения. Они могут быть выявлены лишь в процессе обработки материалов наблюдения. Началом такой обработки и служит сводка и группировка данных наблюдения.
Основным и важнейшим моментом сводки является группировка, т.е. расчленение статистической совокупности на группы и подгруппы по определенным существенным признакам. Выбор группировочного признака – один из самых сложных вопросов теории группировок. После выбора группировочного признака определяется число групп, если оно не указано в условии задания. Определяя число групп, нужно иметь в виду, что в каждую группу должно попасть такое число единиц совокупности, на основании которого можно делать обоснованные выводы.
В результате группировки единиц совокупности по какому-либо варьирующему признаку получают ряды распределения.
Статистическим рядом распределения называют упорядоченное распределение единиц совокупности на группы по изучаемому признаку. В нем различают следующие элементы: варианты (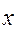 ) и частоты (
) и частоты (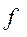 ) или частости (
) или частости (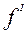 ).
).
Вариантами называют отдельные значения группировочного признака, которые он принимает в ряду распределения. Числа, которые показывают сколько раз (как часто) встречается в ряду распределения то или иное значение варианты, называют частотами. Частость – это относительный показатель структуры совокупности, т.е. он характеризует долю частот отдельных вариант в общей сумме частот. Сумма всех частостей равна единице. Частости могут выражаться и в процентах, тогда сумма всех частостей равна 100 %.
Ряды распределения могут быть построены как по количественному признаку, так и по атрибутивному (не имеющего количественного значения: профессия, пол, отрасль и т.д.). В соответствии с этим ряды делятся на вариационные и атрибутивные. Вариационные ряды могут быть дискретными и интервальными.
Дискретный ряд распределения – это ряд, в котором варианты выражены одним конечным числом (например, группировка рабочих по разряду).
Интервальный ряд – это ряд, в котором значения признака выражены в виде интервала (например, группировка рабочих по уровню заработной платы, стажа).
Интервалом называется разность между максимальным и минимальным значением признака в каждой группе. Причем, интервалы бывают равные (если совокупность более или менее однородная), неравные (если разброс значений признака в совокупности большой), открытые (если нет начального или конечного значения признака в первой или последней группах) и закрытые.
Если строится интервальный ряд с равными интервалами и количество групп оговаривается исследованием, то величина интервала определяется следующим образом:
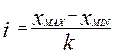 ,
,
где 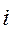 - величина интервала;
- величина интервала;
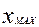 - максимальное значение признака в совокупности;
- максимальное значение признака в совокупности;
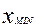 - минимальное значение признака;
- минимальное значение признака;
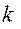 - количество принятых групп.
- количество принятых групп.
Если принимаются неравные интервалы, то следует, чтобы частоты по группам распределялись более менее равномерно.
Результаты группировки оформляются в виде статистической таблицы. Надо уметь правильно построить таблицу и проанализировать ее содержание.
При группировке по одному признаку строятся так называемые групповые таблицы (простой ряд распределения), а при группировке по нескольким признакам – комбинационные таблицы (комбинационное распределение).
Например, группировку рабочих по разряду можно представить в виде следующей таблицы:
Группировка рабочих по разряду (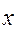 ) )
| Число рабочих (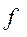 ) )
|
| Итого: |
Группировку рабочих по заработной плате и разряду можно показать с помощью комбинационного распределения:
| Группировка рабочих по зарплате, у.е. | 500- | 520- | 540- | 560- | 580- | Итого |
| Группировка рабочих по разряду | ||||||
| Итого: |
Причем, при построении комбинационного распределения следует количество групп по факториальному признаку брать больше, чем по результативному признаку.
 2015-05-20
2015-05-20 292
292








