Лабораторная работа № 6
«Одноиндексные задачи линейного программирования»
Цель работы
Приобретение навыков построения математических моделей одноиндексных задач ЛП и решения их в Microsoft Excel.
Ход работы
| №вар | |
| D | |
| W | |
| h | |
| Tp1 | 2,4 |
| Tp2 | |
| Tp3 | |
| Tp4 | |
| P1 | |
| P2 | |
| Пр1 | |
| Пр2 | |
| Пр3 | |
| Фв1 | 7,1 |
| Фв2 | 7,5 |
| Фв3 | 7,7 |
| Z1 | |
| Z2 | |
| Z3 | |
| K1 | |
| K2 | |
| V1 | |
| V2 | |
| V3 | |
| N | |
| Ост | |
| Д | 23(А1,В2) |
| З | 80В1 |
| С1 | |
| С2 | |
| С3 | |
| Ц1 | |
| Ц2 | |
| Ц3 |
| цф |
| А | |
| В1 | |
| В2 |
Вывод: нам целесообразно производить тумбочки вида В2. При производстве их количестве 84 шт. мы будем иметь прибыль 128 руб.
Ответы на вопросы:
1. Что такое распределительная задача, общая распределительная задача?
Общая распределительная задача – в которой работы и ресурсы (исполнители) выражаются в различных единицах измерения. Типичным примером такой задачи является организация выпуска разнородной продукции на оборудовании различных типов.
Если в какой-либо системе (экономической, организационной, военной и т.д.) имеющихся в наличии ресурсов не хватает для эффективного выполнения каждой из намеченных работ, то возникают так называемые распределительные задачи.
|
|
|
2. Что такое математическое и линейное программирование?
Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ — область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными.
3. Какова общая форма записи модели ЛП?
В общей форме записи модель задачи ЛП имеет вид:
целевая функция (ЦФ) 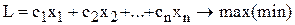 ; при ограничениях ; при ограничениях 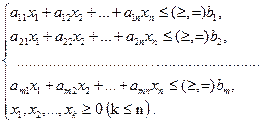 |
4. Что такое допустимое и оптимальное решения?
Допустимое решение – это совокупность чисел 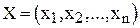 , удовлетворяющих ограничениям задачи.
, удовлетворяющих ограничениям задачи.
Оптимальное решение – это план 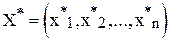 , при котором ЦФ принимает свое максимальное (минимальное) значение.
, при котором ЦФ принимает свое максимальное (минимальное) значение.
5. Каковы основные этапы построения математической модели ЛП?
I этап построения модели заключается в определении (описании, задании, идентификации) переменных. В данной задаче искомыми неизвестными величинами является количество полок каждого вида, которые будут произведены в текущем месяце. Таким образом, 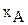 – количество полок А (шт./мес.);
– количество полок А (шт./мес.); 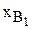 – количество полок В1 (шт./мес.);
– количество полок В1 (шт./мес.); 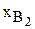 – количество полок В2 (шт./мес.).
– количество полок В2 (шт./мес.).
II этап построения модели заключается в построении целевой функции, представляющей цель решения задачи. В данном случае цель – это максимизация прибыли, получаемой от продажи полок всех видов в течение месяца. Поскольку в этой задаче прибыль может быть определена как разность между ценой (Ц1, Ц2, Ц3) и себестоимостью (С1, С2, С3), то ЦФ имеет вид
|
|
|
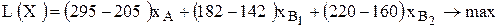 | 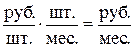 |
III этап построения модели заключается в задании ограничений, моделирующих условия задачи. Все ограничения рассматриваемой задачи можно разделить на несколько типов.
6. Каков экономический смысл и математический вид ЦФ задачи о производстве полок?
 2015-05-10
2015-05-10 1403
1403