Исследование устойчивости автоматических систем управления. Оценка качества регулирования
Цель работы: Применение критериев устойчивости для исследования систем автоматического регулирования, определение показателей качества регулирования систем.
Теоретическая часть
Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.
Определение устойчивости по М.Я.Ляпунову
Невозмущенное движение (при 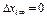 ) называется устойчивым по отношению к переменным
) называется устойчивым по отношению к переменным 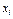 , если при всяком заданном положительном числе
, если при всяком заданном положительном числе 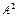 , как бы мало оно не было, можно выбрать другое положительное число
, как бы мало оно не было, можно выбрать другое положительное число 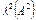 , так, что для всех возмущений
, так, что для всех возмущений 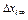 ,, удовлетворяющих условию
,, удовлетворяющих условию 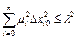 , возмущенное движение будет для времени
, возмущенное движение будет для времени 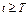 удовлетворять неравенству
удовлетворять неравенству 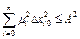 , где
, где 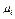 – коэффициенты, уравновешивающие размерности величин
– коэффициенты, уравновешивающие размерности величин 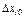 . Если с течением времени
. Если с течением времени 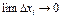 , то система асимптотически устойчива.
, то система асимптотически устойчива.
Устойчивость систем зависит от корней характеристического уравнения. Решение характеристического уравнения есть сумма экспоненциальных функций 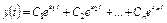 .
.
Рассмотрим варианты свободного движения систем от ненулевого начального положения при различных корнях характеристического уравнения 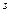 (рисунок 7).
(рисунок 7).
По рисунку 7 можно заметить, что для затухания переходного процесса и устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней были отрицательными, т.е. лежали слева от мнимой оси плоскости корней. Система будет находиться на границе устойчивости при наличии:
1) нулевого корня;
2) пары чисто мнимых корней;
3) бесконечного корня.
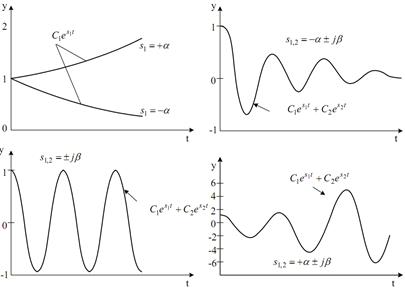
Рисунок 7. Графики движения систем при различных корнях
характеристического уравнения
 2015-05-10
2015-05-10 677
677







