Критерий Рауса-Гурвица используется при анализе устойчивости линейных стационарных систем. Он позволяет аналитически определить, все ли корни полинома имеют отрицательные действительные части.
Вещественные части корней будут отрицательными в том случае, если все коэффициенты уравнения и диагональные миноры главного определителя будут положительными. Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с в возрастающем порядке до 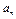 . От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз – с убывающими индексами. Места в матрице коэффициентов с индексами больше
. От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз – с убывающими индексами. Места в матрице коэффициентов с индексами больше 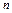 и меньше 0 заполняются нулями.
и меньше 0 заполняются нулями.
Рассмотрим выражение критерия Гурвица для характеристического уравнения третьего порядка 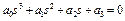 .
.
Главный определитель 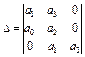 .
.
Условие Гурвица 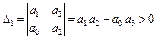 .
.
Следовательно, система будет устойчивой, если все коэффициенты 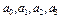 положительны и
положительны и 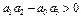 .
.
 2015-05-10
2015-05-10 243
243








