Критерий устойчивости Михайлова. Чтобы все корни характеристического уравнения имели отрицательные вещественные части, необходимо, чтобы после подстановки частоты в соответствующий

Чтобы все корни характеристического уравнения 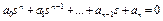имели отрицательные вещественные части, необходимо, чтобы после подстановки частоты в соответствующий характеристический полином 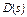полное приращение его фазы при изменении частоты 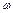от нуля до бесконечности составляло 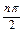, где 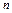– степень полинома 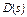. При этом характеристический полином опишет в комплексной плоскости кривую – «годограф Михайлова».

Свойства годографа Михайлова:

1) годограф всегда спиралевиден;

2) при 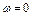, годограф начинается с точки на вещественной оси;

3) годограф уходит в бесконечность при ;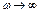

4) при четном 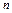, годограф стремится к бесконечности параллельно вещественной оси; при 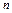– нечетном, годограф стремится к 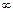параллельно мнимой оси (рисунок 8).

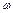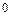Замкнутая система устойчива в том случае, если годограф Михайлова при изменении от до 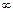проходит в положительном направлении 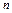квадрантов комплекса плоскости, начиная свое движение от положительной вещественной полуоси, и при этом нигде не обращается в нуль.