Чтобы система в замкнутом состоянии была устойчивой необходимо и достаточно, чтобы при изменении частоты 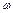 от
от 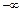 до
до 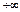 амплитудно-фазовая частотная характеристика разомкнутой системы поворачиваясь вокруг начала координат по часовой стрелке, охватила точку
амплитудно-фазовая частотная характеристика разомкнутой системы поворачиваясь вокруг начала координат по часовой стрелке, охватила точку 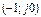 столько раз, сколько корней в правой полуплоскости имеет характеристическое уравнение системы.
столько раз, сколько корней в правой полуплоскости имеет характеристическое уравнение системы.
Примечания
1. Если корней в правой полуплоскости нет, то АФЧХ не должна охватывать точку 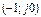 .
.
2. Неустойчивая система в разомкнутом состоянии может быть устойчивой в замкнутом состоянии, и наоборот.
3. АФЧХ всегда начинается на положительной полуоси, но при порядке астатизма r по причине устремления 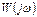 к
к 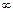 (при
(при 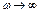 ), видимая часть АФЧХ появляется только в квадранте
), видимая часть АФЧХ появляется только в квадранте 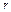 , отсчитанном по часовой стрелке.
, отсчитанном по часовой стрелке.
Примеры АФЧХ для статических САР приведены на рисунке 9:
1 – САР на колебательной границе устойчивости;
2 – абсолютно устойчивая САР;
3 – неустойчивая САР;
4 – условно устойчивая САР (только при изменении 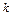 в некотором диапазоне)
в некотором диапазоне)
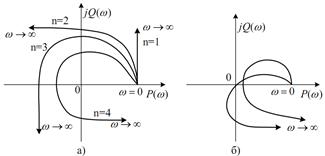
Рисунок 8. Годограф Михайлова: а) для устойчивых систем; б) для неустойчивых систем.
На рисунке 10 показаны АФЧХ астатических САР и САР с чисто мнимыми корнями:
1) устойчивая САР с астатизмом первого порядка;
2) устойчивая САР с астатизмом второго порядка;
3) устойчивая САР с астатизмом третьего порядка;
4) неустойчивая САР с консервативным звеном;
5) устойчивая САР с консервативным звеном (коррекция выполнена фазовращающим звеном).
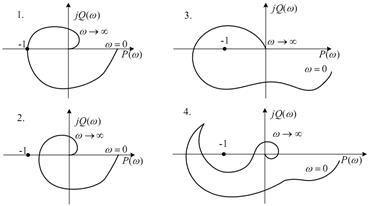
Рисунок 9. Примеры АФЧХ для различных САР
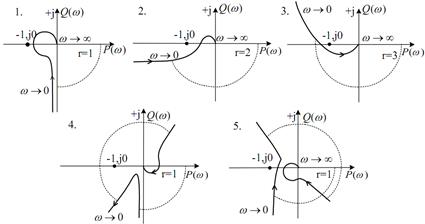
Рисунок 10. Примеры АФЧХ астатических САР и САР с чисто мнимыми корнями
 2015-05-10
2015-05-10 436
436








