с применением определителей Вандермонда

Весьма удобным методом анализа динамики ЭМС с нулевыми начальными условиями является метод определителя Вандермонда, имеющий следующий алгоритм:

1. Записать СДУ, описывающую ЭМС, в нормальной форме Коши.

2. Найти собственные значения 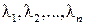матрицы коэффициентов A.

3. Записать полный 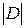и частные 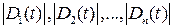определители Вандермонда:

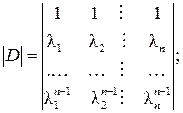
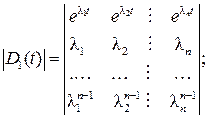
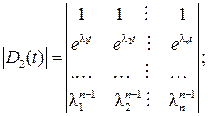
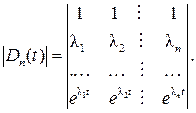
4. Записать матричную функцию F (t):

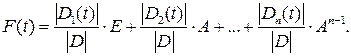
Здесь E – единичная матрица, A – матрица состояния системы.

5. Найти временные характеристики по формуле:

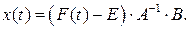
В MathCAD:

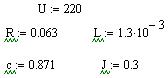
Матрицы коэффициентов и единичная матрица:

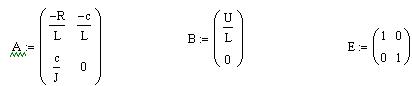
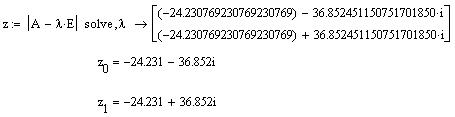
Корни характеристического уравнения:

Матрицы Вандермонда:

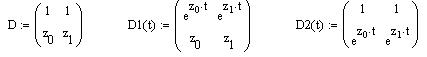
Матричная функция:

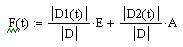
Вектор переменных состояния ДПТ НВ:

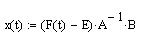
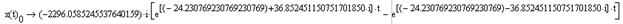
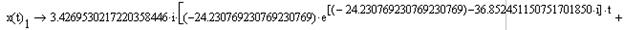
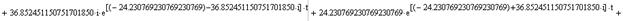
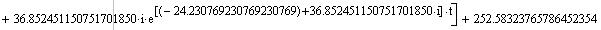
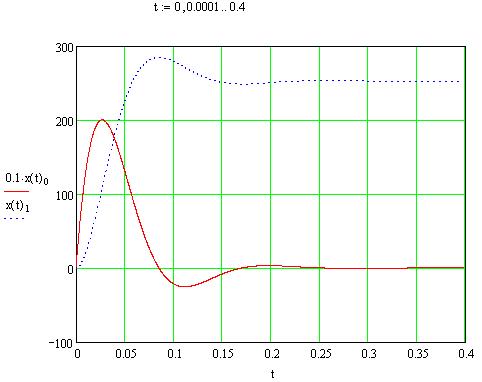
Рис.7. Переходные процессы в ДПТ НВ при решении СДУ

методом определителей Вандермонда

Содержание работы: моделирование работы ДПТ НВ всеми вышеуказанными методами при нулевых и ненулевых начальных условиях (различные динамические режимы – пуск вхолостую, реверс, останов, наброс и сброс номинальной нагрузки).