Вычисление определителей произвольных порядков
Преобразованиями, описанными в разделе 5.1, приводим определитель к треугольному виду. Далее, определитель равен произведению диагональных элементов.
Приведём пример вычисления определителя матрицы 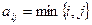 . Вычтем из каждой строки предыдущую (начиная с последней строки). В результате получим треугольную матрицу, по диагонали которой стоят 1. Определитель равен 1.
. Вычтем из каждой строки предыдущую (начиная с последней строки). В результате получим треугольную матрицу, по диагонали которой стоят 1. Определитель равен 1.
Пусть даны числа  . Матрицей Вандермонда называется матрица, у которой на пересечении i-го столбца и j-ой строки расположен элемент, равный
. Матрицей Вандермонда называется матрица, у которой на пересечении i-го столбца и j-ой строки расположен элемент, равный 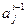 . Обозначим через
. Обозначим через  матрицу Вандермонда. Определитель матрицы Вандермонда является многочленом от
матрицу Вандермонда. Определитель матрицы Вандермонда является многочленом от  , т.к.
, т.к. 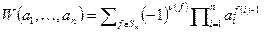 . Рассмотрим определитель как многочлен от
. Рассмотрим определитель как многочлен от  . Степень этого многочлена равна n-1, а его корни равны
. Степень этого многочлена равна n-1, а его корни равны  (т.к. определитель матрицы с двумя одинаковыми строками равен нулю). Следовательно,
(т.к. определитель матрицы с двумя одинаковыми строками равен нулю). Следовательно, 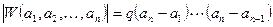 , где q – коэффициент при старшей степени. Легко убедиться, что
, где q – коэффициент при старшей степени. Легко убедиться, что 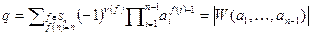 . Таким образом получена рекуррентная формула
. Таким образом получена рекуррентная формула  , последовательным применением которой придём к равенству
, последовательным применением которой придём к равенству 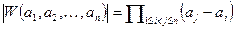 .
.
 2014-02-02
2014-02-02 3423
3423
