2015-05-10
391
Лабораторная работа №8
Линейное программирование
Решение транспортной задачи
Постановка задачи:
Имеется m поставщиков, которые обозначены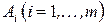 
, у которых сосредоточен однородный груз в количестве 
.
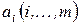Груз требуется перевезти n потребителям обозначенных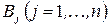 
в количестве 
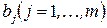. Также известна стоимость перевозок от i -го поставщика j -тому потребителю, выраженной матрицей
,
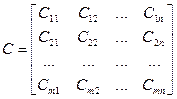где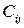 
− стоимость перевозки 1 единицы груза от i -того поставщика j ‑тому потребителю.
Требуется составить такой план перевозки груза, при котором, общая стоимость перевозки будет минимальной. Для удобства решения сведем данные задачи в следующую таблицу:
| Потребитель Поставщик |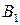 
| 
| … | 
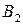
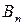
| Запасы |
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
| … | … | … | … | … | … |
| 
| 
| … | 
| 
|
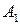
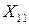
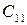
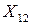
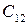
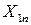
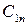
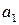
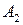
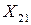
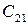
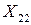
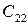
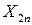
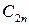
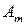
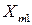
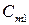
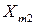
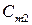
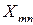
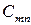
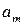
| Потребности |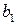 
| 
| … | 
|
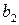
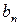
Введем неизвестное в задаче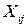 
− количество груза, которое необходимо перевезти от i -того поставщика к j -тому потребителю.
Таким образом, можно сформулировать математическую постановку задачи:
|
|
|
Требуется найти минимум функции цели (целевая функция):
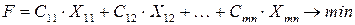
Функция F представляет собой общую стоимость всего перевозимого груза при следующих ограничениях:
1) ограничения на потребности
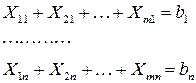
2) ограничения на запасы
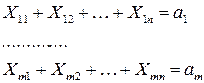
3) количество груза не может быть отрицательным, также может быть наложено условие, чтобы Х представлялось целым числом.
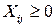, целое.
