В соответствии с номером бригады необходимо выбрать заданные для расчета параметры и тип фильтра из таблицы 1. Во всех вариантах рассчитывается фильтр нижних частот (ФНЧ).
Таблица 1
| № бригады
|
|
|
|
|
|
| fgpp, кГц
|
|
|
|
|
|
| Apmax, дБ
| 1.3
| 1.3
|
| 1.2
| 1.2
|
| Apmin, дБ
|
|
|
|
|
|
| Тип фильтра
| Чебышева
| Баттерворта
| Чебышева
| Баттерворта
| Чебышева
|
| fd, кГц
|
|
|
|
|
|
| fgpn, кГц
|
|
|
|
|
|
Продолжение таблицы 1
| № бригады
|
|
|
|
|
|
| fgpp, кГц
|
|
|
|
|
|
| Apmax, дБ
| 1.4
| 0.9
| 0.9
| 1.1
| 1.2
|
| Apmin, дБ
|
|
|
|
|
|
| Тип фильтра
| Баттерворта
| Чебышева
| Баттерворта
| Чебышева
| Баттерворта
|
| fd, кГц
|
|
|
|
|
|
| fgpn, кГц
|
|
|
|
|
|
Продолжение таблицы 1
| № бригады
|
|
|
|
|
|
| fgpp, кГц
|
|
|
|
|
|
| Apmax, дБ
| 1.4
| 1.5
| 0.9
| 1.1
| 1.2
|
| Apmin, дБ
|
|
|
|
|
|
| Тип фильтра
| Чебышева
| Баттерворта
| Чебышева
| Баттерворта
| Чебышева
|
| fd, кГц
|
|
|
|
|
|
| fgpn, кГц
|
|
|
|
|
|
В таблице 1 введены обозначения:
fgpp - граничная частота полосы пропускания в кГц;
fgpn - граничная частота полосы непропускания в кГц;
fd - частота дискретизации в кГц.
Далее следует для выбранного варианта в программной среде «Mathcad» произвести расчет АЧХ, ФЧХ и 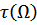 аналогового ФНЧ прототипа.
аналогового ФНЧ прототипа.
Выполнив билинейное Z преобразование необходимо произвести расчет АЧХ, ФЧХ и 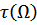 для цифрового ФНЧ.
для цифрового ФНЧ.
При расчете в среде «Mathcad», в первую очередь в рабочем поле файла необходимо описать все константы, переменные и функции, которые в дальнейшем будут использоваться при расчетах.
После расчета характеристик цифрового фильтра необходимо определить его структуру. Для этого записывается системная функция фильтра в развернутом виде, подставляя вместо 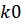 и Т конкретные значения, а также рассчитанные ранее значения полюсов:
и Т конкретные значения, а также рассчитанные ранее значения полюсов:
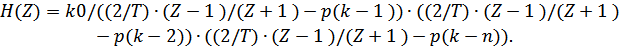
Последующие действия производятся с использованием символьного процессора.
Из меню «символы» выбирается пункт «расчеты/символические». Преобразуемое выражение для 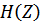 выделяется синей рамкой и производятся следующие действия, выбирая соответствующие пункты из меню «символы»:
выделяется синей рамкой и производятся следующие действия, выбирая соответствующие пункты из меню «символы»:
· «расчеты /символические» - символическая оценка всего выражения;
· «упростить» - упрощение всего выражения;
· «расширить» - разложение выражения, выделив числитель;
· «расширить» - разложение выражения, выделив знаменатель.
Полученное выражение будет представлять собой дробно-рациональное выражение 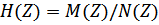 , где
, где 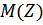 и
и 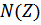 - полиномы от
- полиномы от 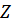 в положительных степенях. Далее необходимо привести полученную системную функцию к виду, удобному для реализации ЦФ. Для этого необходимо вынести за скобки
в положительных степенях. Далее необходимо привести полученную системную функцию к виду, удобному для реализации ЦФ. Для этого необходимо вынести за скобки 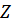 в максимальной степени из числителя и знаменателя и сократить на нее. После этого получим
в максимальной степени из числителя и знаменателя и сократить на нее. После этого получим 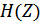 в виде (например)
в виде (например)
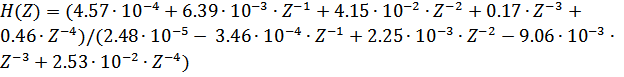 .
.
Согласно полученному выражению можно построить структурную схему фильтра, причем выражение в числителе представляет собой прямую (нерекурсивную) часть фильтра, а знаменатель - рекурсивную.
| (пример расчета цифрового ФНЧ Баттерворта)
|
| fd - частота дискритизации (Гц)
|
| fc - частота среза (Гц), равна половине fd
|
| fв - верхняя частота звукового сигнала (Гц)
|
| k0 - константа нормирования
|
| HA(w) - передаточная функция аналового фильтра
|
| H(w) - передаточная функция дискретного фильтра
|
| βАw - ФЧХ аналогового фильтра, град
|
| βw - ФЧХ цифрового фильтра, град
|
| τА(w) - групповая задержка аналогового фильтра
|
| τ(w) - групповая задержка дискретного фильтра
|
| ε- параметр, характеризующий пульсации в полосе пропускания
|
| k0 - константа нормирования
|
| wn - нормированная частота
|
| Amin - требуемое затухание на частоте среза Fp (дБ)
|
| Amax - допустимая неравномерность в полосе пропускания (дБ)
|
| Неравномерность в полосе пропускания определяется по формуле:
|
| Порядок фильтра определяется по формуле:
|
| Округление порядка фильтра в большую сторону производится с помощью функции:
|
| Период дискретизации определяется по формуле:
|
| Полюсы функции определяются по формуле:
|
| Передаточная функция аналогового фильтра определяется по формуле:
|
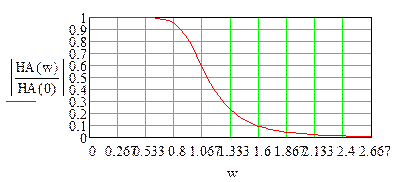
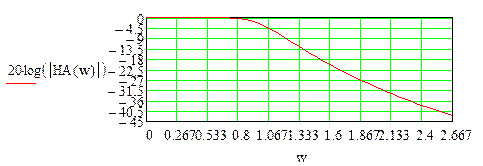
| Рисунок П1 - АЧХ аналогового ФНЧ Баттерворта
|
| Рабочее затухание аналогового фильтра определяется по формуле:
|
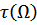 аналогового ФНЧ прототипа.
аналогового ФНЧ прототипа.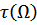 для цифрового ФНЧ.
для цифрового ФНЧ.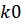 и Т конкретные значения, а также рассчитанные ранее значения полюсов:
и Т конкретные значения, а также рассчитанные ранее значения полюсов: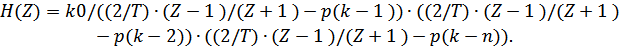
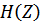 выделяется синей рамкой и производятся следующие действия, выбирая соответствующие пункты из меню «символы»:
выделяется синей рамкой и производятся следующие действия, выбирая соответствующие пункты из меню «символы»: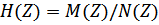 , где
, где 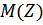 и
и 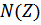 - полиномы от
- полиномы от 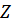 в положительных степенях. Далее необходимо привести полученную системную функцию к виду, удобному для реализации ЦФ. Для этого необходимо вынести за скобки
в положительных степенях. Далее необходимо привести полученную системную функцию к виду, удобному для реализации ЦФ. Для этого необходимо вынести за скобки 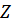 в максимальной степени из числителя и знаменателя и сократить на нее. После этого получим
в максимальной степени из числителя и знаменателя и сократить на нее. После этого получим 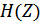 в виде (например)
в виде (например)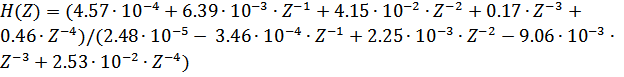 .
.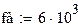
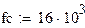
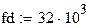
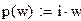
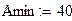
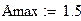
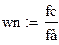
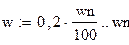
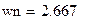
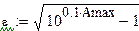
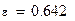
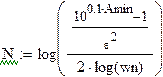
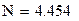
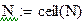
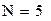
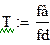
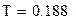
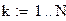
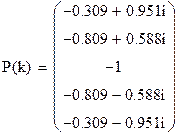
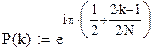
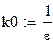
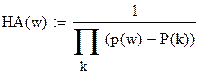
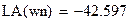
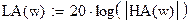
 2015-05-10
2015-05-10 408
408








