Метод билинейного преобразования

Билинейное преобразование представляет собой конформное отображение точек р-плоскости в точки наz - плоскости и использует замены вида: ;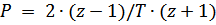

где 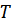- период частоты дискретизации, на которой работает цифровой фильтр.

Билинейное преобразование обеспечивает однозначное преобразование переда­точной функции 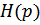аналогового фильтра-прототипа в передаточную функ­цию 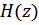цифрового фильтра: .

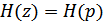Рассмотрим это преобразование.

Каждой точке комплексной р-плоскости (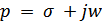) ставится в соответствие определенная точка z-плоскости ().

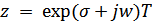Мнимая ось р-плоскости (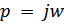) для 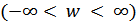отображается в единичную окружность вz-плоскости (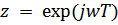). Левая половина р-плоскости ото­бражается в часть z-плоскости внутри единичного круга .

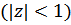Очень важными являются два обстоятельства.

Во-первых, поскольку все полюсы устойчивого аналогового фильтра распо­ложены в левой половине р-плоскости, то при преобразовании аналогового фильтра к цифровому получается также устойчивый фильтр.

Во-вторых, так как мнимая ось р-плоскости отображается на единичную окружность z-плоскости, то все максимумы и минимумы АЧХ 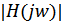анало­гового фильтра сохраняется и в АЧХ 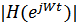цифрового фильтра.

Сохраняется также неравномерность АЧХ для соответствующих диапазонов частот.

Таким образом, избирательные аналоговые фильтры преобразуются в соответ­ствующие цифровые фильтры.

Соотношение между «аналоговыми» частотами 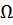и «цифровыми» частотами 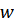определяется уравнением

;

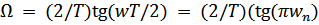где 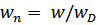- нормированная относительно частоты дискретизации «цифро­вая» частота.

Перечислим последовательность этапов расчета ЦФ методом билинейного пре­образования.

1. Перевести требуемые характеристики и нормы ЦФ в соответствующие требования к АФ, применяя формулу:

,

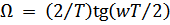где w - реальная частота, т.е. частота проектируемого ЦФ,

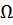- расчетная частота, т.е. частота вспомогательного АФ.

2. Рассчитать передаточную функцию АФ 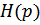, применяя методы расчета ана­логовых фильтров.

3. Определить передаточную функцию ЦФ 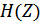по известной .

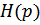4. Построить схему ЦФ по .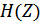

5. Выполнить необходимые расчеты по учету эффектов конечной разрядности.

В данной лабораторной работе будем использовать аппроксимацию характе­ристик фильтров полиномами Баттерворта и Чебышева.